题目内容
已知函数 ,函数
,函数 的导函数
的导函数 ,且
,且 ,其中
,其中 为自然对数的底数.
为自然对数的底数.
(1)求 的极值;
的极值;
(2)若 ,使得不等式
,使得不等式 成立,试求实数
成立,试求实数 的取值范围;
的取值范围;
(1)当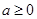 时,
时, 没有极值;当
没有极值;当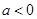 时,
时, 存在极大值,且当
存在极大值,且当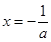 时,
时, ;(2)
;(2) .
.
解析试题分析:(1)对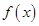 求导可得
求导可得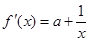
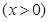 ,由极值定义可知要对
,由极值定义可知要对 进行分类讨论,当
进行分类讨论,当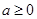 ,
, ,函数无极值,当
,函数无极值,当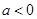 时,可得当
时,可得当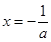 存在极大值;(2) 由函数
存在极大值;(2) 由函数 的导函数
的导函数 ,且
,且 ,得
,得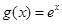 ,可知不等式
,可知不等式 变为
变为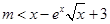 ,求出
,求出
 的取值范围,可得m的范围.
的取值范围,可得m的范围.
解:(1) 函数 的定义域为
的定义域为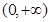 ,
,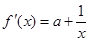
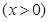 .
.
当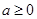 时,
时, ,
, 在
在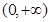 上为增函数,
上为增函数, 没有极值;当
没有极值;当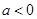 时,
时,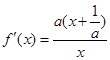 ,
,
若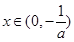 时,
时, ;若
;若 时,
时,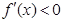
 存在极大值,且当
存在极大值,且当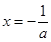 时,
时,
综上可知:当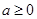 时,
时, 没有极值;当
没有极值;当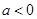 时,
时, 存在极大值,且当
存在极大值,且当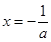 时,
时,
(2) 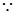 函数
函数 的导函数
的导函数 ,
,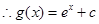
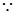
 ,
,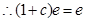
 ,
,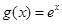
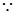
 ,使得不等式
,使得不等式 成立,
成立,
 ,使得
,使得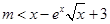 成立,
成立,
对于 ,
, ,由于
,由于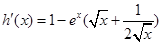 ,
,
当 时,
时,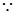
 ,
,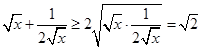 ,
,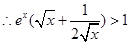 ,
,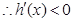 ,从而
,从而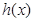 在
在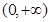 上为减函数,
上为减函数,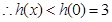
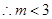
考点:1.导数的运算;2.函数的极值.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
 ,其中
,其中 .
. 在点
在点 处的切线方程为
处的切线方程为 ,求函数
,求函数 的解析式;
的解析式; ,不等式
,不等式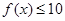 在
在 上恒成立,求
上恒成立,求 的取值范围.
的取值范围.
 ,函数
,函数
 时,求函数
时,求函数 的表达式;
的表达式; ,函数
,函数 上的最小值是2 ,求
上的最小值是2 ,求 的值;
的值; 与函数
与函数 ,求F(x)=f(x)-g(x)的单调区间;
,求F(x)=f(x)-g(x)的单调区间; 元,并且每件产品需向总公司交
元,并且每件产品需向总公司交 元(
元( )时,一年的销售量为
)时,一年的销售量为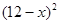 万件.
万件. (万元)与每件产品的售价
(万元)与每件产品的售价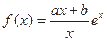 (
( ).
).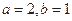 ,求函数
,求函数 的极值;
的极值; .
. 时,对任意
时,对任意 ,都有
,都有 成立,求
成立,求 的最大值;
的最大值; 的导函数.若存在
的导函数.若存在 ,使
,使 成立,求
成立,求 的取值范围.
的取值范围. ,证明数列{an}成等比数列,并求数列{xn}的通项公式;
,证明数列{an}成等比数列,并求数列{xn}的通项公式;