题目内容
设函数f(x)=mx2-mx-1.
(1)若对于一切实数x,f(x)<0恒成立,求m的取值范围;
(2)若对于x∈[1,3],f(x)<-m+5恒成立,求m的取值范围.
解:(1)要使mx2-mx-1<0恒成立,
若m=0,显然-1<0;
若m≠0,则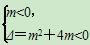 ⇒-4<m<0.
⇒-4<m<0.
所以-4<m≤0.
(2)要使f(x)<-m+5在[1,3]上恒成立,即
m 2+
2+ m-6<0在x∈[1,3]上恒成立.
m-6<0在x∈[1,3]上恒成立.
有以下两种方法:
法一:令g(x)=m 2+
2+ m-6,x∈[1,3].
m-6,x∈[1,3].
当m>0时,g(x)在[1,3]上是增函数,
所以g(x)max=g(3)⇒7m-6<0,
所以m< ,则0<m<
,则0<m< ;
;
当m=0时,-6<0恒成立;
当m<0时,g(x)在[1,3]上是减函数,
所以g(x)max=g(1)⇒m-6<0,所以m<6,所以m<0.
综上所述:m的取值范围是 .
.
法二:因为x2-x+1= 2+
2+ >0,
>0,
又因为m(x2-x+1)-6<0,
所以m< .
.
因为函数y= 在[1,3]上的最小值为
在[1,3]上的最小值为 ,所以只需m<
,所以只需m< 即可.所以,m的取值范围是
即可.所以,m的取值范围是 .
.

练习册系列答案
相关题目
 ,
, 满足
满足 ,则
,则 __________.
__________. 值为( )
值为( ) B.
B.  C.
C.  D.
D. 


 ,则f(-1)=( )
,则f(-1)=( )
 f(0) D.f(0),f(3)
f(0) D.f(0),f(3) 在[0,2]上单调递增,且函数
在[0,2]上单调递增,且函数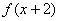 是偶函数,则下列结论成立的是( )
是偶函数,则下列结论成立的是( )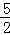 )<f(
)<f(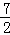 ) B.f(
) B.f(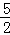 )
)