题目内容
18.过圆x2+y2=1外一点A(2,0)作圆的割线,求割线被圆截得的弦的中点的轨迹方程.分析 设弦BC中点(x,y),过A的直线的斜率为k,求得割线ABC的方程.再由弦的中点与圆心连线与割线ABC垂直可得垂线的方程.再根据弦的中点是这两条直线的交点,求出弦的中点的轨迹方程.
解答 解:设弦BC中点(x,y),过A的直线的斜率为k,则割线ABC的方程:y=k(x-2).
作圆的割线ABC,所以弦的中点与圆心连线与割线ABC垂直,垂线的方程为:x+ky=0.
因为交点就是弦的中点,它在这两条直线上,故弦BC中点的轨迹方程是:x2+y2-2x=0,
即(x-1)2+y2=1(已知圆内部分).
点评 本题考查形式数形结合的数学思想,轨迹方程,直线与圆的方程的应用,中档题.

练习册系列答案
 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案 天天练口算系列答案
天天练口算系列答案
相关题目
8.扇形的半径是6cm,圆心角为15°,则扇形面积是( )
| A. | $\frac{π}{2}c{m^2}$ | B. | 3πcm2 | C. | πcm2 | D. | $\frac{3π}{2}c{m^2}$ |
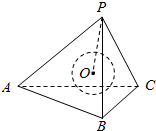 正三棱锥高为1,底面边长为2$\sqrt{6}$,内有一球与四个面都相切.
正三棱锥高为1,底面边长为2$\sqrt{6}$,内有一球与四个面都相切.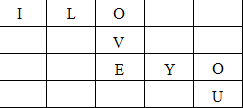 将“I LOVE YOU”8个英文字母填入5×4的方格中,其中“I“字母填入左上角,“U”字母填入右下角,将其余6个英文字母依次填入方格,要求只能横读或竖读成一句原话,如图所示为一种填法,则共有35种不同的填法.(用数字作答)
将“I LOVE YOU”8个英文字母填入5×4的方格中,其中“I“字母填入左上角,“U”字母填入右下角,将其余6个英文字母依次填入方格,要求只能横读或竖读成一句原话,如图所示为一种填法,则共有35种不同的填法.(用数字作答)