题目内容
(本题满分13分)在直角坐标平面内,以坐标原点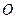 为极点,
为极点,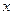 轴的正半轴为极轴,建立极坐标系.曲线
轴的正半轴为极轴,建立极坐标系.曲线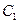 的极坐标方程是
的极坐标方程是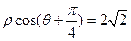 ,曲线
,曲线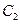 的参数方程是
的参数方程是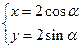 (
(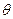 为参数,
为参数,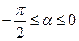
 ),求曲线
),求曲线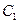 上的点和曲线
上的点和曲线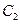 上的点之间距离的取值范围.
上的点之间距离的取值范围.
 为极点,
为极点, 轴的正半轴为极轴,建立极坐标系.曲线
轴的正半轴为极轴,建立极坐标系.曲线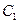 的极坐标方程是
的极坐标方程是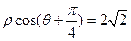 ,曲线
,曲线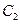 的参数方程是
的参数方程是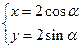 (
(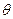 为参数,
为参数,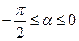
 ),求曲线
),求曲线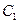 上的点和曲线
上的点和曲线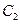 上的点之间距离的取值范围.
上的点之间距离的取值范围.曲线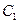 上的点和曲线
上的点和曲线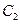 上的点之间的距离的取值范围是
上的点之间的距离的取值范围是
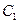 上的点和曲线
上的点和曲线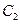 上的点之间的距离的取值范围是
上的点之间的距离的取值范围是
解:由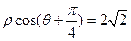 得曲线
得曲线 的直角坐标方程为
的直角坐标方程为 ,是一直线 ................3分
,是一直线 ................3分
由 化简得
化简得 ,又
,又 ,∴
,∴ ,
,
∴曲线 的直角坐标方程为
的直角坐标方程为 (
( ,
, ),它是以原点为圆心,半径为
),它是以原点为圆心,半径为 ,在第四象限的四分之一圆 ................5分
,在第四象限的四分之一圆 ................5分
∴圆心到直线 的距离
的距离
由图像可知,当直线与四分之一圆 相切时,曲线
相切时,曲线 上的点和曲线
上的点和曲线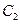 上的点之间的距离最短,最短距离为
上的点之间的距离最短,最短距离为 .................8分
.................8分
当取曲线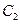 上的点为
上的点为 或
或 时,曲线
时,曲线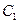 上的点和曲线
上的点和曲线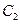 上的点之间的距离最长,此时点
上的点之间的距离最长,此时点 或
或 到直线的距离为
到直线的距离为 ................11分
................11分
∴曲线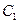 上的点和曲线
上的点和曲线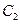 上的点之间的距离的取值范围是
上的点之间的距离的取值范围是 ................13分
................13分
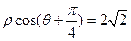 得曲线
得曲线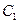 的直角坐标方程为
的直角坐标方程为 ,是一直线 ................3分
,是一直线 ................3分由
 化简得
化简得 ,又
,又 ,∴
,∴ ,
,
∴曲线
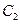 的直角坐标方程为
的直角坐标方程为 (
( ,
, ),它是以原点为圆心,半径为
),它是以原点为圆心,半径为 ,在第四象限的四分之一圆 ................5分
,在第四象限的四分之一圆 ................5分∴圆心到直线
 的距离
的距离
由图像可知,当直线与四分之一圆
 相切时,曲线
相切时,曲线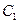 上的点和曲线
上的点和曲线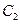 上的点之间的距离最短,最短距离为
上的点之间的距离最短,最短距离为 .................8分
.................8分当取曲线
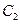 上的点为
上的点为 或
或 时,曲线
时,曲线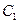 上的点和曲线
上的点和曲线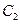 上的点之间的距离最长,此时点
上的点之间的距离最长,此时点 或
或 到直线的距离为
到直线的距离为 ................11分
................11分∴曲线
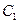 上的点和曲线
上的点和曲线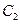 上的点之间的距离的取值范围是
上的点之间的距离的取值范围是 ................13分
................13分
练习册系列答案
相关题目
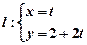 (参数
(参数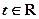 )与曲线
)与曲线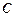 的极坐标方程为
的极坐标方程为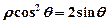
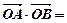 0.
0. ,曲线C的参数方程为
,曲线C的参数方程为 为参数),求曲线C截直线l所得的弦长.
为参数),求曲线C截直线l所得的弦长. 的参数方程:
的参数方程: (
( 为参数)和圆
为参数)和圆 的极坐标方程:
的极坐标方程: .
.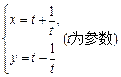 相交于A、B两点.求线段AB的长.
相交于A、B两点.求线段AB的长. ,则该曲线的参数方程为_______________.
,则该曲线的参数方程为_______________. 表示同一条曲线的参数方程(t为参数)是 ( )
表示同一条曲线的参数方程(t为参数)是 ( )





 则普通方程为 ( )
则普通方程为 ( )  为参数,0≤
为参数,0≤ <2π),
<2π), 轴非负半轴为极轴的极坐标系下的极坐标方程.
轴非负半轴为极轴的极坐标系下的极坐标方程.