题目内容
已知数列{an}是等差数列,数列{bn}是正项等比数列,且满足a1=1,b1=4,a2+b2=10,a26-b3=10.
(1)求数列{an},{bn}的通项公式;
(2)记cn=anbn,求数列{Cn}的前n项和Sn.
(1)求数列{an},{bn}的通项公式;
(2)记cn=anbn,求数列{Cn}的前n项和Sn.
考点:数列的求和,等差数列的通项公式,等比数列的通项公式
专题:等差数列与等比数列
分析:(1)由已知得
,由此能求出an=1+n-1=n,bn=4•2n-1=2n+1.
(2)由cn=anbn=n•2n+1.利用错位相减法能求出数列{cn}的前n项和Sn.
|
(2)由cn=anbn=n•2n+1.利用错位相减法能求出数列{cn}的前n项和Sn.
解答:
解:(1)∵数列{an}是等差数列,数列{bn}是正项等比数列,
且满足a1=1,b1=4,a2+b2=10,a26-b3=10.
∴
,
解得d=1,q=2,
∴an=1+n-1=n,
bn=4•2n-1=2n+1.
(2)∵cn=anbn=n•2n+1.
∴Sn=1•22+2•23+3•24+…+n•2n+1,①
2Sn=1•23+2•24+3•25+…+n•2n+2,②
①-②,得:-Sn=22+23+24+…+2n+1-n•2n+2
=
-n•2n+2
=(1-n)•2n+2-4,
∴Sn=(n-1)•2n+2+4.
且满足a1=1,b1=4,a2+b2=10,a26-b3=10.
∴
|
解得d=1,q=2,
∴an=1+n-1=n,
bn=4•2n-1=2n+1.
(2)∵cn=anbn=n•2n+1.
∴Sn=1•22+2•23+3•24+…+n•2n+1,①
2Sn=1•23+2•24+3•25+…+n•2n+2,②
①-②,得:-Sn=22+23+24+…+2n+1-n•2n+2
=
| 4(1-2n) |
| 1-2 |
=(1-n)•2n+2-4,
∴Sn=(n-1)•2n+2+4.
点评:本题考查数列的通项公式的求法,考查数列的前n项和的求法,是中档题,解题时要认真审题,注意错位相减法的合理运用.

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目
已知直线x-y+a=0与圆x2+y2=4交于不同两点A、B,O为坐标原点,若向量
、
满足|
+
|=|
-
|,则a=( )
| OA |
| OB |
| OA |
| OB |
| OA |
| OB |
| A、±1 | ||
| B、±2 | ||
C、±
| ||
D、±
|
设p:m>6;q:m2>36,则是¬p是¬q的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分又不必要条件 |
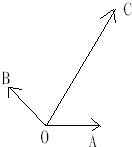 如图,|
如图,|