题目内容
14.已知函数f(x)=2x,若x1,x2是R上的任意两个数,且x1≠x2,则$\frac{{{2^{x_1}}+{2^{x_2}}}}{2}>{2^{\frac{{{x_1}+{x_2}}}{2}}}$,请对比函数f(x)=2x得到函数g(x)=lgx一个类似的结论:x1,x2是R上的任意两个数,且x1≠x2,则$\frac{{2}^{{x}_{1}}+{2}^{{x}_{2}}}{2}<{2}^{\frac{{x}_{1}+{x}_{2}}{2}}$.分析 由题意函数f(x)=2x,是一个凹函数,函数g(x)=lgx,是一个凸函数,即可得出结论.
解答 解:由题意函数f(x)=2x,是一个凹函数,函数g(x)=lgx,是一个凸函数,
∴x1,x2是R上的任意两个数,且x1≠x2,则$\frac{{2}^{{x}_{1}}+{2}^{{x}_{2}}}{2}<{2}^{\frac{{x}_{1}+{x}_{2}}{2}}$.
故答案为:x1,x2是R上的任意两个数,且x1≠x2,则$\frac{{2}^{{x}_{1}}+{2}^{{x}_{2}}}{2}<{2}^{\frac{{x}_{1}+{x}_{2}}{2}}$.
点评 本题考查函数的性质,考查类比推理,考查学生分析解决问题的能力,比较基础.

练习册系列答案
相关题目
19. 如图在正方体ABCD-A1B1C1D1中,E,F分别是棱CC1,BC的中点,则直线EF与直线D1C所成角的大小是( )
如图在正方体ABCD-A1B1C1D1中,E,F分别是棱CC1,BC的中点,则直线EF与直线D1C所成角的大小是( )
 如图在正方体ABCD-A1B1C1D1中,E,F分别是棱CC1,BC的中点,则直线EF与直线D1C所成角的大小是( )
如图在正方体ABCD-A1B1C1D1中,E,F分别是棱CC1,BC的中点,则直线EF与直线D1C所成角的大小是( )| A. | 30° | B. | 45° | C. | 60° | D. | 90° |
3.已知抛物线y2=8x的准线与双曲线$\frac{x^2}{a^2}-\frac{y^2}{16}$=1相交于A,B两点,点F为抛物线的焦点,△ABF为直角三角形,则双曲线的离心率为( )
| A. | 3 | B. | 2 | C. | $\sqrt{6}$ | D. | $\sqrt{3}$ |
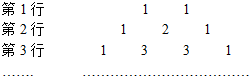 如图,在杨辉三角中,若某行存在相邻的三个数成等差数列,则称此行为“A-P行”.从上往下数,第1个A-P行的行序号是7,第k个A-P行的行序号是(k+2)2-2.
如图,在杨辉三角中,若某行存在相邻的三个数成等差数列,则称此行为“A-P行”.从上往下数,第1个A-P行的行序号是7,第k个A-P行的行序号是(k+2)2-2.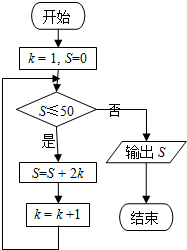
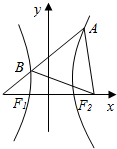 如图,F1,F2是双曲线的左、右焦点,过F1的直线l与双曲线的左右两支分别交于点B、A两点,若△ABF2为等边三角形,则该双曲线的离心率为$\sqrt{7}$.
如图,F1,F2是双曲线的左、右焦点,过F1的直线l与双曲线的左右两支分别交于点B、A两点,若△ABF2为等边三角形,则该双曲线的离心率为$\sqrt{7}$.