题目内容
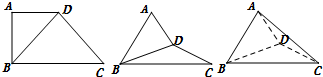
11. 如图,已知△ABC中,D为BC的中点,AE=$\frac{1}{2}$EC,AD,BE交于点F,设$\overrightarrow{AC}$=$\overrightarrow{a}$,$\overrightarrow{AD}$=$\overrightarrow{b}$.
如图,已知△ABC中,D为BC的中点,AE=$\frac{1}{2}$EC,AD,BE交于点F,设$\overrightarrow{AC}$=$\overrightarrow{a}$,$\overrightarrow{AD}$=$\overrightarrow{b}$.(1)用$\overrightarrow{a}$,$\overrightarrow{b}$分别表示向量$\overrightarrow{AB}$,$\overrightarrow{EB}$;
(2)若$\overrightarrow{AF}$=t$\overrightarrow{AD}$,求实数t的值.
分析 (1)利用向量的线性运算,即可用$\overrightarrow{a}$,$\overrightarrow{b}$分别表示向量$\overrightarrow{AB}$,$\overrightarrow{EB}$;
(2)若$\overrightarrow{AF}$=t$\overrightarrow{AD}$,利用$\overrightarrow{FB}$,$\overrightarrow{EB}$共线,求实数t的值.
解答 解:(1)由题意,D为BC的中点,且$\overrightarrow{AE}$=$\frac{1}{3}$$\overrightarrow{AC}$,
∵$\overrightarrow{AB}$+$\overrightarrow{AC}$=2$\overrightarrow{AD}$,
∴$\overrightarrow{AB}$=2$\overrightarrow{b}$-$\overrightarrow{a}$,
∴$\overrightarrow{EB}$=$\overrightarrow{AB}$-$\overrightarrow{AE}$=2$\overrightarrow{b}$-$\overrightarrow{a}$-$\frac{1}{3}$$\overrightarrow{a}$=-$\frac{4}{3}$$\overrightarrow{a}$+2$\overrightarrow{b}$;
(2)∵$\overrightarrow{AF}$=t$\overrightarrow{AD}$=t$\overrightarrow{b}$,
∴$\overrightarrow{FB}$=$\overrightarrow{AB}$-$\overrightarrow{AF}$=-$\overrightarrow{a}$+(2-t)$\overrightarrow{b}$,
∵$\overrightarrow{EB}$=-$\frac{4}{3}$$\overrightarrow{a}$+2$\overrightarrow{b}$,$\overrightarrow{FB}$,$\overrightarrow{EB}$共线,
∴$\frac{-1}{-\frac{4}{3}}=\frac{2-t}{2}$,
∴t=$\frac{1}{2}$.
点评 本题考查向量的线性运算,考查向量共线条件的运用,属于中档题.

| A. | -2 | B. | -4 | C. | -6 | D. | -10 |
| A. | (0,3) | B. | (-$\frac{1}{2}$,2) | C. | (-$\frac{2}{3}$,4) | D. | (-$\frac{5}{9}$,3) |
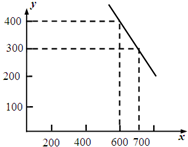 某公司试销一种成本单价为500元/件的新产品,规定试销时销售单价不低于成本单价,又不高于800元/件.经试销调查,发现销售量y(件)与销售单价x(元/件)可近似看作一次函数y=kx+b的关系(如图所示).
某公司试销一种成本单价为500元/件的新产品,规定试销时销售单价不低于成本单价,又不高于800元/件.经试销调查,发现销售量y(件)与销售单价x(元/件)可近似看作一次函数y=kx+b的关系(如图所示).