题目内容
10．函数y=f（2x-1）是偶函数，则函数y=f（2x+1）的对称轴是（ ）| A． | x=-1 | B． | x=0 | C． | $x=\frac{1}{2}$ | D． | $x=-\frac{1}{2}$ |
分析 根据偶函数的图象关于y轴对称，利用图象的变换规律，即可求得函数y=f（2x+1）的对称轴．
解答 解：∵函数y=f（2x-1）是偶函数，∴函数的图象关于y轴对称
∵函数y=f（2x+1）是由函数y=f（2x-1）的图象向左平移1个单位得到，
∴函数y=f（2x+1）的对称轴是直线x=-1，
故选：A．
点评 本题考查偶函数图象的对称性，考查图象的变换，考查学生分析解决问题的能力，属于基础题．
练习册系列答案
相关题目
18．设条件p：x＞0，条件q：x＞1，则条件p是条件q的（ ）
| A． | 充分不必要条件 | B． | 必要不充分条件 | ||
| C． | 充要条件 | D． | 非充分非必要条件 |
5．若向量$\overrightarrow{a}$，$\overrightarrow{b}$满足|$\overrightarrow{a}$|=$\sqrt{3}$，|$\overrightarrow{b}$|=2，$\overrightarrow{a}$⊥（$\overrightarrow{a}$-$\overrightarrow{b}$），则$\overrightarrow{a}$与$\overrightarrow{b}$的夹角为（ ）
| A． | $\frac{π}{2}$ | B． | $\frac{2π}{3}$ | C． | $\frac{π}{6}$ | D． | $\frac{5π}{6}$ |
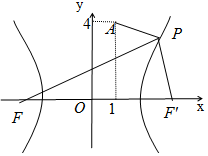已知F是双曲线C：$\frac{x^2}{4}-\frac{y^2}{12}=1$的左焦点，A（1，4），P是双曲线右支上的动点．求：