题目内容
画出函数y=2sin( x-
x- )的一个周期的图象(要求具有数量特征),并且写出由函数y=sinx变化到函数y=2sin(
)的一个周期的图象(要求具有数量特征),并且写出由函数y=sinx变化到函数y=2sin( x-
x- )的变化流程图;
)的变化流程图;
列表:
| x | |||||
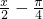 | |||||
 |

Sinx→
 →
→ →
→ .
.
解:已知函数
(I)五点法画出函数在长度为一个周期的闭区间上的简图;

(II)变化流程图
指出此函数的图象可以由y=sinx的图象经过怎样的变换得到,
y=sinx 横坐标扩大2倍 得到y= 图象向右平移
图象向右平移 个单位得到y=
个单位得到y= ,纵坐标扩大为原来的2倍得到y=
,纵坐标扩大为原来的2倍得到y=
分析:(I)利用正弦函数的图象性质,将内层函数看作整体等于正弦曲线的五个关键点,列出表格,再描点、连线即可
(II)利用三角函数图象变换理论,可先将正弦曲线进行横向伸缩,再将所得图象进行横向平移,最后进行纵向伸缩,按顺序写明变换量即可
点评:本题考查了三角函数的图象和性质,五点作图法的原理和操作步骤,图象变换的理论等基础知识

(I)五点法画出函数在长度为一个周期的闭区间上的简图;
| X |  |  |  | 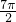 |  |
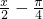 | 0 |  | π |  | 2π |
 | 0 | 2 | 0 | -2 | 0 |

(II)变化流程图
指出此函数的图象可以由y=sinx的图象经过怎样的变换得到,
y=sinx 横坐标扩大2倍 得到y=
 图象向右平移
图象向右平移 个单位得到y=
个单位得到y= ,纵坐标扩大为原来的2倍得到y=
,纵坐标扩大为原来的2倍得到y=
分析:(I)利用正弦函数的图象性质,将内层函数看作整体等于正弦曲线的五个关键点,列出表格,再描点、连线即可
(II)利用三角函数图象变换理论,可先将正弦曲线进行横向伸缩,再将所得图象进行横向平移,最后进行纵向伸缩,按顺序写明变换量即可
点评:本题考查了三角函数的图象和性质,五点作图法的原理和操作步骤,图象变换的理论等基础知识

练习册系列答案
相关题目


 的一条对称轴为直线
的一条对称轴为直线
 上的简图.
上的简图.