题目内容
函数y=2sin（2x+φ）（0＜φ＜
）的一条对称轴为直线x=
．
（1）求φ；
（2）求该函数对称中心、单调区间；
（3）在图上画出函数y=2sin（2x+φ）在[-
，
]上的简图．
| π |
| 2 |
| π |
| 12 |
（1）求φ；
（2）求该函数对称中心、单调区间；
（3）在图上画出函数y=2sin（2x+φ）在[-
| π |
| 6 |
| 5π |
| 6 |
分析：（1）由题意可知函数在x=
处取得最值，从而可得φ；
（2）令2x+
=kπ可得对称中心，由2kπ-
≤2x+
≤2kπ+
，得函数的增区间，由2kπ+
≤2x+
≤2kπ+
，得函数的减区间；
（3）利用“五点法”可作出函数图象，列表、描点、连线；
| π |
| 12 |
（2）令2x+
| π |
| 3 |
| π |
| 2 |
| π |
| 3 |
| π |
| 2 |
| π |
| 2 |
| π |
| 3 |
| 3π |
| 2 |
（3）利用“五点法”可作出函数图象，列表、描点、连线；
解答：解：（1）∵函数的一条对称轴为直线x=
，
∴2sin（2×
+φ）=±2，则
+φ=kπ+
，k∈Z，
又0＜φ＜
，∴φ=
；
（2）由（1）知，y=2sin（2x+
），
令2x+
=kπ，得x=
-
，k∈Z，
∴该函数的对称中心为（
-
，0）；
由2kπ-
≤2x+
≤2kπ+
，得kπ-
≤x≤kπ+
，k∈Z，
∴该函数的增区间为[kπ-
，kπ+
]；
由2kπ+
≤2x+
≤2kπ+
，得kπ+
≤x≤kπ+
，k∈Z，
∴该函数的减区间为[kπ+
，kπ+
]；
（3）如下图 列表、描点、连线．
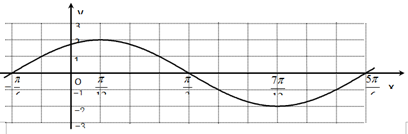
| π |
| 12 |
∴2sin（2×
| π |
| 12 |
| π |
| 6 |
| π |
| 2 |
又0＜φ＜
| π |
| 2 |
| π |
| 3 |
（2）由（1）知，y=2sin（2x+
| π |
| 3 |
令2x+
| π |
| 3 |
| kπ |
| 2 |
| π |
| 6 |
∴该函数的对称中心为（
| kπ |
| 2 |
| π |
| 6 |
由2kπ-
| π |
| 2 |
| π |
| 3 |
| π |
| 2 |
| 5π |
| 12 |
| π |
| 12 |
∴该函数的增区间为[kπ-
| 5π |
| 12 |
| π |
| 12 |
由2kπ+
| π |
| 2 |
| π |
| 3 |
| 3π |
| 2 |
| π |
| 12 |
| 7π |
| 12 |
∴该函数的减区间为[kπ+
| π |
| 12 |
| 7π |
| 12 |
（3）如下图 列表、描点、连线．
点评：本题考查y=Asin（ωx+φ）的图象作法、解析式的求解及其单调性，属中档题，熟练掌握三角函数的图象和性质是解决问题的关键．
练习册系列答案
相关题目
函数y=2sin(2x+
)是（ ）
| π |
| 2 |
| A、周期为π的奇函数 |
| B、周期为π的偶函数 |
| C、周期为2π的奇函数 |
| D、周期为2π的偶函数 |