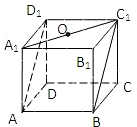
题目内容
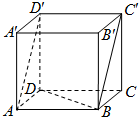
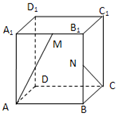
如图,在侧棱垂直底面的四棱柱ABCD-A1B1C1D1中,AD∥BC,AD⊥AB,AB=
.AD=2,BC=4,AA1=2,E是DD1的中点,F是平面B1C1E与直线AA1的交点.
(1)证明:
(i)EF∥A1D1;
(ii)BA1⊥平面B1C1EF;
(2)求BC1与平面B1C1EF所成的角的正弦值.
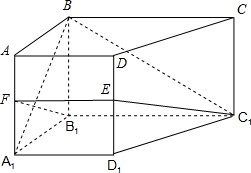
| 2 |
(1)证明:
(i)EF∥A1D1;
(ii)BA1⊥平面B1C1EF;
(2)求BC1与平面B1C1EF所成的角的正弦值.

(1)证明(i)∵C1B1∥A1D1,C1B1?平面ADD1A1,∴C1B1∥平面ADD1A1,
又C1B1?平面B1C1EF,平面B1C1EF∩平面ADD1A1=EF,
∴C1B1∥EF,∴EF∥A1D1;
(ii)∵BB1⊥平面A1B1C1D1,∴BB1⊥B1C1,
又∵B1C1⊥B1A1,
∴B1C1⊥平面ABB1A1,
∴B1C1⊥BA1,
在矩形ABB1A1中,F是AA1的中点,tan∠A1B1F=tan∠AA1B=
,即∠A1B1F=∠AA1B,故BA1⊥B1F.
所以BA1⊥平面B1C1EF;
(2)设BA1与B1F交点为H,
连接C1H,由(1)知BA1⊥平面B1C1EF,所以∠BC1H是BC1与平面B1C1EF所成的角.
在矩形AA1B1B中,AB=
,AA1=2,得BH=
,
在RT△BHC1中,BC1=2
,sin∠BC1H=
=
,
所以BC1与平面B1C1EF所成的角的正弦值是
.
又C1B1?平面B1C1EF,平面B1C1EF∩平面ADD1A1=EF,
∴C1B1∥EF,∴EF∥A1D1;
(ii)∵BB1⊥平面A1B1C1D1,∴BB1⊥B1C1,
又∵B1C1⊥B1A1,
∴B1C1⊥平面ABB1A1,
∴B1C1⊥BA1,

在矩形ABB1A1中,F是AA1的中点,tan∠A1B1F=tan∠AA1B=
| ||
| 2 |
所以BA1⊥平面B1C1EF;
(2)设BA1与B1F交点为H,
连接C1H,由(1)知BA1⊥平面B1C1EF,所以∠BC1H是BC1与平面B1C1EF所成的角.
在矩形AA1B1B中,AB=
| 2 |
| 4 | ||
|
在RT△BHC1中,BC1=2
| 5 |
| BH |
| BC1 |
| ||
| 15 |
所以BC1与平面B1C1EF所成的角的正弦值是
| ||
| 15 |

练习册系列答案
相关题目