题目内容
如图，四棱锥S-ABCD的底面是正方形，SD⊥平面ABCD，SD=AD=2．
（1）求证：SA⊥CD；
（2）求异面直线SB与CD所成角的大小．
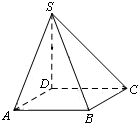
（1）求证：SA⊥CD；
（2）求异面直线SB与CD所成角的大小．
（1）∵SD⊥平面ABCD，CD⊆平面ABCD，∴CD⊥SD，
又∵四边形ABCD是正方形，∴CD⊥AD，
又SD∩AD=D，∴CD⊥平面SDA，
又∵SA⊆平面SDA，∴SA⊥CD
（2）∵四边形ABCD是正方形，∴AB‖CD，
∴∠SBA或其补角是异面直线SB与CD所成角，
由（1）知BA⊥平面SDA，∴△SAB是直角三角形
∴tan∠SBA=
=
=
，
∴∠SBA=arctan
，
故异面直线SB与CD所成角的大小为arctan
．
又∵四边形ABCD是正方形，∴CD⊥AD，
又SD∩AD=D，∴CD⊥平面SDA，
又∵SA⊆平面SDA，∴SA⊥CD
（2）∵四边形ABCD是正方形，∴AB‖CD，
∴∠SBA或其补角是异面直线SB与CD所成角，
由（1）知BA⊥平面SDA，∴△SAB是直角三角形
∴tan∠SBA=
| SA |
| AD |
2
| ||
| 2 |
| 2 |
∴∠SBA=arctan
| 2 |
故异面直线SB与CD所成角的大小为arctan
| 2 |
练习册系列答案
培优口算题卡系列答案
开心口算题卡系列答案
口算题卡河北少年儿童出版社系列答案
相关题目
