题目内容

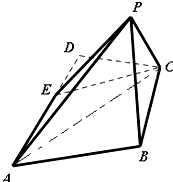
已知四面体ABCD的六条棱长都是1，则直线AD与平面ABC的夹角的余弦值为______．
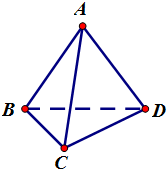
设D点底面ABC上的投影为E，则E为△ABC的中心
连接AE、DE，则∠DAE即为直线AD与平面ABC的夹角
∵四面体ABCD的六条棱长都是1，
∴AE=
3
3
，
则cos∠DAE=
AE
AD
=
3
3

故答案为：
3
3
．
练习册系列答案
相关题目
已知A、B、C是球O的球面上三点，∠BAC=90°，AB=2，BC=4，球O的表面积为48π，则异面直线AB与OC所成角余弦值为______．
如图，在侧棱垂直底面的四棱柱ABCD-A1B1C1D1中，AD∥BC，AD⊥AB，AB=
2
．AD=2，BC=4，AA1=2，E是DD1的中点，F是平面B1C1E与直线AA1的交点．
（1）证明：
（i）EF∥A1D1；
（ii）BA1⊥平面B1C1EF；
（2）求BC1与平面B1C1EF所成的角的正弦值．
下图是几何体ABC-A1B1C1的三视图和直观图．M是CC1上的动点，N，E分别是AM，A1B1的中点．
（1）求证：NE∥平面BB1C1C；
（2）当M在CC1的什么位置时，B1M与平面AA1C1C所成的角是30°．
已知正四面体ABCD的棱长为a，点O是△BCD的中心，点M是CD中点．
（1）求点A到面BCD的距离；
（2）求AB与面BCD所成角的正弦值．
已知正方体ABCD-A1B1C1D1，则直线AB与平面BDA1所成角的正弦值等于______．
如图，在四边形ABCD中，AB=AD=4，BC=CD=
7
，点E为线段AD上的一点．现将△DCE沿线段EC翻折到PAC，使得平面PAC⊥平面ABCE，连接PA，PB．
（Ⅰ）证明：BD⊥平面PAC；
（Ⅱ）若∠BAD=60°，且点E为线段AD的中点，求直线PE与平面ABCE所成角的正弦值．
在正方体ABCD-A1B1C1D1中，BC1与平面BDD1B1所成的角为（　　）
A．30°B．45°C．60°D．90°
如图，△ABC是等腰直角三角形∠ACB=90°，AC=2a，D，E分别为AC，AB的中点，沿DE将△ADE折起，得到如图所示的四棱锥A′-BCDE
（Ⅰ）在棱A′B上找一点F，使EF∥平面A′CD；
（Ⅱ）当四棱锥A'-BCDE体积取最大值时，求平面A′CD与平面A′BE夹角的余弦值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网