题目内容
已知向量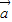 =(1,sinx),
=(1,sinx),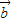 =(sin2x,cosx),函数f(x)=
=(sin2x,cosx),函数f(x)=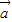 •
•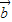 ,x∈[0,
,x∈[0,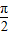 ]
](Ⅰ)求f(x)的最小值;
(Ⅱ)若f(a)=
 ,求sin2a的值.
,求sin2a的值.
【答案】分析:(Ⅰ)把向量的坐标代入数量及公式后进行化积运算,然后根据给出的x的范围求向量数量积的最小值;
(Ⅱ)把f(a)= 代入(Ⅰ)中的表达式求出
代入(Ⅰ)中的表达式求出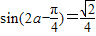 ,根据角的范围求出
,根据角的范围求出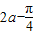 的余弦值,利用配角运算求sin2a的值.
的余弦值,利用配角运算求sin2a的值.
解答:解:(Ⅰ)由向量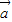 =(1,sinx),
=(1,sinx),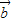 =(sin2x,cosx),
=(sin2x,cosx),
所以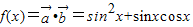 =
=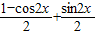 =
=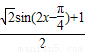
因为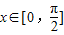 ,所以
,所以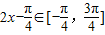 ,
,
当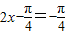 ,即x=0时,f(x)有最小值0;
,即x=0时,f(x)有最小值0;
(Ⅱ)由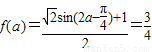 ,得
,得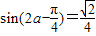
∵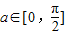 ,
,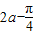
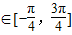 ,又0<
,又0<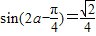 <
<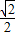
∴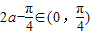 ,得
,得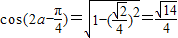 .
.
∴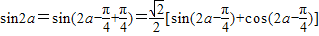
=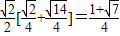 .
.
点评:本题考查了平面向量的数量积的运算,考查了学生的计算能力,解答的关键在于配角思想的应用,同时注意三角函数中给值求值时角的范围的限制,是中档题.
(Ⅱ)把f(a)=
 代入(Ⅰ)中的表达式求出
代入(Ⅰ)中的表达式求出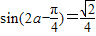 ,根据角的范围求出
,根据角的范围求出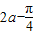 的余弦值,利用配角运算求sin2a的值.
的余弦值,利用配角运算求sin2a的值.解答:解:(Ⅰ)由向量
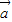 =(1,sinx),
=(1,sinx),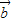 =(sin2x,cosx),
=(sin2x,cosx),所以
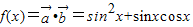 =
=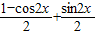 =
=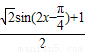
因为
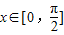 ,所以
,所以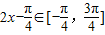 ,
,当
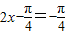 ,即x=0时,f(x)有最小值0;
,即x=0时,f(x)有最小值0;(Ⅱ)由
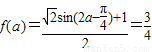 ,得
,得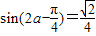
∵
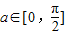 ,
,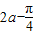
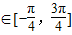 ,又0<
,又0<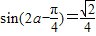 <
<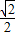
∴
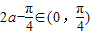 ,得
,得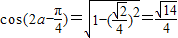 .
.∴
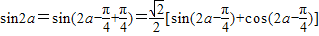
=
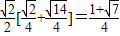 .
.点评:本题考查了平面向量的数量积的运算,考查了学生的计算能力,解答的关键在于配角思想的应用,同时注意三角函数中给值求值时角的范围的限制,是中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目