题目内容
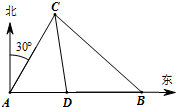 如图所示,港口A北偏东30°方向的点C处有一观测站,港口正东方向的B处有一轮船,测得BC为31海里.该轮船从B处沿正西方向航行20海里后到达D处,测得CD为21海里.问此时轮船离港口A还有多少海里?
如图所示,港口A北偏东30°方向的点C处有一观测站,港口正东方向的B处有一轮船,测得BC为31海里.该轮船从B处沿正西方向航行20海里后到达D处,测得CD为21海里.问此时轮船离港口A还有多少海里?分析:在△BDC中,先由余弦定理可得,可求cos∠CDB,进而可求sin∠CDB,由三角形的内角和定理可得sin∠ACD=sin(∠CDB-
),再在△ACD中,由正弦定理知,
=
,可求AD
| π |
| 3 |
| AD |
| sin∠ACD |
| CD |
| sin∠A |
解答: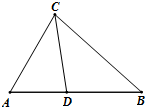 解:由题意可得,BC=31,BD=20,CD=21,A=60°
解:由题意可得,BC=31,BD=20,CD=21,A=60°
在△BCD中,由余弦定理得cos∠BDC=
=
=-
,
故sin∠BDC=
=
,
从而sin∠ACD=sin(∠BDC-60°)=sin∠BDCcos60°-cos∠BDCsin60°=
×
-(-
)×
=
.
在△ACD中,由正弦定理得
=
,
于是AD=
=15(海里),
即此时轮船距离港口A还有 15海里.
 解:由题意可得,BC=31,BD=20,CD=21,A=60°
解:由题意可得,BC=31,BD=20,CD=21,A=60°在△BCD中,由余弦定理得cos∠BDC=
| BD2+CD2-BC2 |
| 2×BD×CD |
| 202+212-312 |
| 2×21×20 |
| 1 |
| 7 |
故sin∠BDC=
| 1-cos2∠BDC |
4
| ||
| 7 |
从而sin∠ACD=sin(∠BDC-60°)=sin∠BDCcos60°-cos∠BDCsin60°=
4
| ||
| 7 |
| 1 |
| 2 |
| 1 |
| 7 |
| ||
| 2 |
5
| ||
| 14 |
在△ACD中,由正弦定理得
| AD |
| sin∠ACD |
| CD |
| sin60° |
于是AD=
| CD×sin∠ACD |
| sin60° |
即此时轮船距离港口A还有 15海里.
点评:本题主要考查了正弦定理、余弦定理、两角差的正弦公式及三角形的内角和定理在实际中的应用,解决实际的问题的关键是要把题目中所提供的数据转化成数学图形中的长度(角度),然后根据相应的公式来解决问题.

练习册系列答案
相关题目
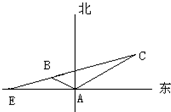 如图所示,某海岛上一观察哨A上午11时测得一轮船在海岛北偏东60°的C处,12时20分测得船在海岛北偏西60°的B处,12时40分轮船到达位于海岛正西方且距海岛5km的E港口,如果轮船始终匀速直线前进,问船速多少?
如图所示,某海岛上一观察哨A上午11时测得一轮船在海岛北偏东60°的C处,12时20分测得船在海岛北偏西60°的B处,12时40分轮船到达位于海岛正西方且距海岛5km的E港口,如果轮船始终匀速直线前进,问船速多少?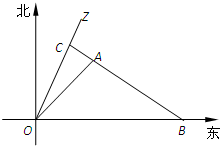 如图所示,一科学考察船从港口O出发,沿北偏东α角的射线OZ方向航行,而在离港口
如图所示,一科学考察船从港口O出发,沿北偏东α角的射线OZ方向航行,而在离港口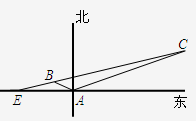 如图所示,上午11时在某海岛上一观察点A测得一轮船在海岛北偏东60°的C处,12时20分测得船在海岛北偏西60°的B处,12时40分轮船到达了位于海岛正西方且距海岛5km的E港口,轮船始终以匀速直线前进.
如图所示,上午11时在某海岛上一观察点A测得一轮船在海岛北偏东60°的C处,12时20分测得船在海岛北偏西60°的B处,12时40分轮船到达了位于海岛正西方且距海岛5km的E港口,轮船始终以匀速直线前进. 出发,沿北偏东
出发,沿北偏东 角的射线
角的射线 方向航行,而在离港口
方向航行,而在离港口 (
( 为正常数)海里的北偏东
为正常数)海里的北偏东 角的A处有一个供给科考船物资的小岛,其中
角的A处有一个供给科考船物资的小岛,其中 ,
, .现指挥部需要紧急征调沿海岸线港口
.现指挥部需要紧急征调沿海岸线港口 )海里的B处的补给船,速往小岛A装运物资供给科考船,该船沿BA方向全速追赶科考船,并在C处相遇.经测算当两船运行的航向与海岸线OB围成的三角形OBC的面积最小时,这种补给最适宜.
)海里的B处的补给船,速往小岛A装运物资供给科考船,该船沿BA方向全速追赶科考船,并在C处相遇.经测算当两船运行的航向与海岸线OB围成的三角形OBC的面积最小时,这种补给最适宜. ;
;