题目内容
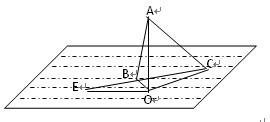
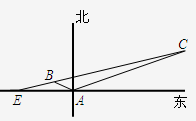
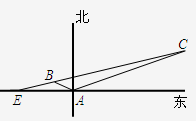如图所示，上午11时在某海岛上一观察点A测得一轮船在海岛北偏东60°的C处，12时20分测得船在海岛北偏西60°的B处，12时40分轮船到达了位于海岛正西方且距海岛5km的E港口，轮船始终以匀速直线前进．（Ⅰ）求观测点A与B之间的距离；
（Ⅱ）求轮船的速度．
分析：（Ⅰ）根据题意，可知BC=4BE，设BE=xkm，则BC=4xkm在三角形EAC中，由正弦定理求得sinC，再在△ABC中，由正弦定理，求得AB即可得出观测点A与B之间的距离；
（Ⅱ）先△ABE中，由余弦定理，得BE的长，从而得出船速即可．
（Ⅱ）先△ABE中，由余弦定理，得BE的长，从而得出船速即可．
解答：解：（Ⅰ）依题意，上午11时在某海岛上一观察点A测得一轮船在海岛北偏东60°的C处，12时20分测得船在海岛北偏西60°的B处，12时40分轮船到达了位于海岛正西方且距海岛5km的E港口，轮船始终以匀速直线前进．
可知BC=4BE（1分）
设BE=xkm，则BC=4xkm
由已知，得∠BAE=30°，∠EAC=150°，
由正弦定理得
=
，所以sinC=
=
=
（5分）
在△ABC中，由正弦定理，得
=
，（7分）
∴AB=
=
=
．（9分）
所以观测点A与B之间的距离为
km（10分）
（Ⅱ）△ABE中，由余弦定理，得BE2=AB2+AE2-2AB•AE•cos30°=
+25-2×
×5×
=
（13分）
所以船速v=
=
=
（14分）
答：该船的速度为
km/h（15分）
可知BC=4BE（1分）
设BE=xkm，则BC=4xkm
由已知，得∠BAE=30°，∠EAC=150°，
由正弦定理得
| EC |
| sin∠EAC |
| AE |
| sinC |
| AE•sinEAC |
| EC |
| 5sin150° |
| 5x |
| 1 |
| 2x |
在△ABC中，由正弦定理，得
| BC |
| sin120° |
| AB |
| sinC |
∴AB=
| BC•sinC |
| sin120° |
4x•
| ||||
|
4
| ||
| 3 |
所以观测点A与B之间的距离为
4
| ||
| 3 |
（Ⅱ）△ABE中，由余弦定理，得BE2=AB2+AE2-2AB•AE•cos30°=
| 16 |
| 3 |
4
| ||
| 3 |
| ||
| 2 |
| 31 |
| 3 |
所以船速v=
| BE |
| t |
| ||||
|
| 93 |
答：该船的速度为
| 93 |
点评：本题是中档题，考查利用正弦定理、余弦定理在实际问题中的应用，注意选择正确的三角形以及合理的定理解答是解好题目的关键，考查计算能力．
练习册系列答案
相关题目
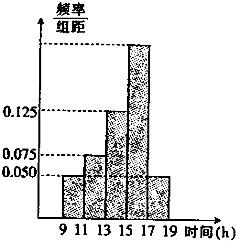某商场在春节黄金周的促销活动中，对每天上午9时至下午19时的销售额进行统计，其频率分布直方图如图所示，已知9时至11时的销售额为2万元，则从15时至17时的销售额为
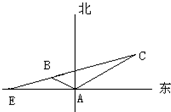如图所示，某海岛上一观察哨A上午11时测得一轮船在海岛北偏东60°的C处，12时20分测得船在海岛北偏西60°的B处，12时40分轮船到达位于海岛正西方且距海岛5km的E港口，如果轮船始终匀速直线前进，问船速多少？
