题目内容
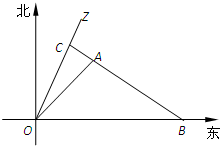 如图所示,一科学考察船从港口O出发,沿北偏东α角的射线OZ方向航行,而在离港口
如图所示,一科学考察船从港口O出发,沿北偏东α角的射线OZ方向航行,而在离港口| 13 |
| 1 |
| 3 |
| 2 | ||
|
| 7 |
| 3 |
(1)求S关于m的函数关系式S(m);
(2)应征调m为何值处的船只,补给最适宜.
分析:先以O为原点,正北方向为轴建立直角坐标系.
(1)先求出直线OZ的方程,然后根据β的正余弦值和OA的距离求出A的坐标,进而可以得到直线AB的方程,然后再与直线OZ的方程联立求出C点的坐标,根据三角形的面积公式可得到答案.
(2)根据(1)中S(m)的关系式,进行变形整理,然后利用基本不等式求出最小值.
(1)先求出直线OZ的方程,然后根据β的正余弦值和OA的距离求出A的坐标,进而可以得到直线AB的方程,然后再与直线OZ的方程联立求出C点的坐标,根据三角形的面积公式可得到答案.
(2)根据(1)中S(m)的关系式,进行变形整理,然后利用基本不等式求出最小值.
解答:解:以O为原点,正北方向为轴建立直角坐标系,直线OZ的方程为y=3x①,
(1)设A(x0,y0),∵cosβ=cosβ=
,∴sinβ=
,
则x0=
asinβ=3a,y0=
acosβ=2a,∴A(3a,2a).
又B(m,0),则直线AB的方程为y=
(x-m) ②
由①、②解得,C(
,
),
∴S(m)=S△OBC=
|OB||yc|=
×m×
=
(m>
a).
(2)S(m)=
=a[(m-
a)+
+
a]≥
当且仅当m-
a=
,即m=
a时,等号成立,
故当m=
a海里时,补给最适宜.
(1)设A(x0,y0),∵cosβ=cosβ=
| 2 | ||
|
| 3 | ||
|
则x0=
| 13 |
| 13 |
又B(m,0),则直线AB的方程为y=
| 2a |
| 3a-m |
由①、②解得,C(
| 2am |
| 3m-7a |
| 6am |
| 3m-7a |
∴S(m)=S△OBC=
| 1 |
| 2 |
| 1 |
| 2 |
| 6am |
| 3m-7a |
| 3am2 |
| 3m-7a |
| 7 |
| 3 |
(2)S(m)=
| 3am2 |
| 3m-7a |
| 7 |
| 3 |
| 49a2 | ||
9(m-
|
| 14 |
| 3 |
| 28a2 |
| 3 |
当且仅当m-
| 7 |
| 3 |
| 49a2 | ||
9(m-
|
| 14 |
| 3 |
故当m=
| 14 |
| 3 |
点评:本题考查解三角形的实际应用、三角形的面积公式、基本不等式的应用,解题的关键是函数的建模思想和转化思想.

练习册系列答案
相关题目
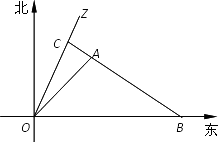
 出发,沿北偏东
出发,沿北偏东 角的射线
角的射线 方向航行,而在离港口
方向航行,而在离港口 (
( 为正常数)海里的北偏东
为正常数)海里的北偏东 角的A处有一个供给科考船物资的小岛,其中
角的A处有一个供给科考船物资的小岛,其中 ,
, .现指挥部需要紧急征调沿海岸线港口
.现指挥部需要紧急征调沿海岸线港口 )海里的B处的补给船,速往小岛A装运物资供给科考船,该船沿BA方向全速追赶科考船,并在C处相遇.经测算当两船运行的航向与海岸线OB围成的三角形OBC的面积最小时,这种补给最适宜.
)海里的B处的补给船,速往小岛A装运物资供给科考船,该船沿BA方向全速追赶科考船,并在C处相遇.经测算当两船运行的航向与海岸线OB围成的三角形OBC的面积最小时,这种补给最适宜. ;
;
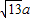 (a为正常数)海里的北偏东β角的A处有一个供给科考船物资的小岛,其中
(a为正常数)海里的北偏东β角的A处有一个供给科考船物资的小岛,其中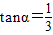 ,
,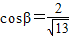 .现指挥部需要紧急征调沿海岸线港口O正东m(
.现指挥部需要紧急征调沿海岸线港口O正东m(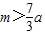 )海里的B处的补给船,速往小岛A装运物资供给科考船,该船沿BA方向全速追赶科考船,并在C处相遇.经测算当两船运行的航向与海岸线OB围成的三角形OBC的面积最小时,这种补给最适宜.
)海里的B处的补给船,速往小岛A装运物资供给科考船,该船沿BA方向全速追赶科考船,并在C处相遇.经测算当两船运行的航向与海岸线OB围成的三角形OBC的面积最小时,这种补给最适宜.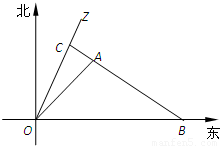
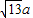 (a为正常数)海里的北偏东β角的A处有一个供给科考船物资的小岛,其中
(a为正常数)海里的北偏东β角的A处有一个供给科考船物资的小岛,其中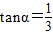 ,
,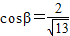 .现指挥部需要紧急征调沿海岸线港口O正东m(
.现指挥部需要紧急征调沿海岸线港口O正东m(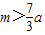 )海里的B处的补给船,速往小岛A装运物资供给科考船,该船沿BA方向全速追赶科考船,并在C处相遇.经测算当两船运行的航向与海岸线OB围成的三角形OBC的面积最小时,这种补给最适宜.
)海里的B处的补给船,速往小岛A装运物资供给科考船,该船沿BA方向全速追赶科考船,并在C处相遇.经测算当两船运行的航向与海岸线OB围成的三角形OBC的面积最小时,这种补给最适宜.