题目内容
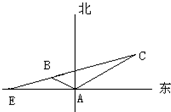如图所示，某海岛上一观察哨A上午11时测得一轮船在海岛北偏东60°的C处，12时20分测得船在海岛北偏西60°的B处，12时40分轮船到达位于海岛正西方且距海岛5km的E港口，如果轮船始终匀速直线前进，问船速多少？
分析：依题意得，设EB=x，则BC=4x，由已知得∠BAE=30°，∠EAC=150°．在△AEC中，利用正弦定理求出sinC；在△ABC中，在△ABC中，由正弦定理求出AB；在△ABE中，由余弦定理得BE．最后得到结果．
解答：解：轮船从C到B用时80分钟，从B到E用时20分钟，
而船始终匀速前进，由此可见：BC=4EB，设EB=x，
则BC=4x，由已知得∠BAE=30°，∠EAC=150°
在△AEC中，由正弦定理得：
sinC=
=
=
在△ABC中，由正弦定理得：AB=
=
=
在△ABE中，由余弦定理得：BE2=AB2+AE2-2AB•AEcos30°=
所以船速 v=
=
=
答：该船的速度
km/h
而船始终匀速前进，由此可见：BC=4EB，设EB=x，
则BC=4x，由已知得∠BAE=30°，∠EAC=150°
在△AEC中，由正弦定理得：
sinC=
| AEsin∠EAC |
| EC |
| 5sin150° |
| 5x |
| 1 |
| 2x |
在△ABC中，由正弦定理得：AB=
| BCsinC |
| sin120° |
4x•
| ||||
|
4
| ||
| 3 |
在△ABE中，由余弦定理得：BE2=AB2+AE2-2AB•AEcos30°=
| 31 |
| 3 |
所以船速 v=
| BE |
| t |
| ||||
|
| 93 |
答：该船的速度
| 93 |
点评：本题是中档题，考查利用正弦定理、余弦定理在实际问题中的应用，注意选择正确的三角形以及合理的定理解答是解好题目的关键，考查计算能力．
练习册系列答案
优等生题库系列答案
相关题目
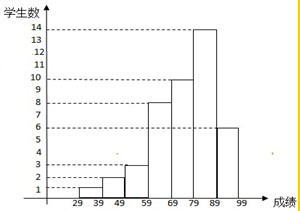如图所示是某班学生一次数学考试成绩的频数分布直方图，其中纵轴表示学生数，观察图形，回答下列问题：
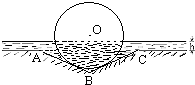（2012•徐汇区一模）某种型号汽车的四个轮胎半径相同，均为R=40cm，该车的底盘与轮胎中心在同一水平面上．该车的涉水安全要求是：水面不能超过它的底盘高度．如图所示：某处有一“坑形”地面，其中坑ABC形成顶角为120°的等腰三角形，且AB=BC=60cm，如果地面上有h（cm）（h＜40）高的积水（此时坑内全是水，其它因素忽略不计）．
