题目内容
(本小题满分12分)
已知抛物线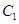 :
: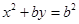 经过椭圆
经过椭圆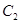 :
: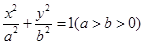 的两个焦点.设
的两个焦点.设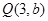 ,又
,又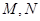 为
为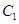 与
与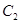 不在
不在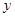 轴上的两个交点,若
轴上的两个交点,若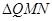 的重心(中线的交点)在抛物线
的重心(中线的交点)在抛物线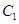 上,
上,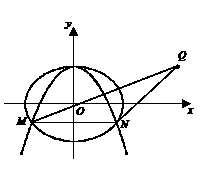
(1)求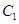 和
和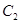 的方程.
的方程.
(2)有哪几条直线与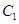 和
和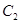 都相切?(求出公切线方程)
都相切?(求出公切线方程)
(1) 抛物线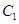 的方程为:
的方程为: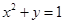 , 椭圆
, 椭圆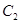 的方程为:
的方程为: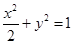
(2) 有3条直线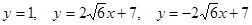 与
与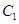 和
和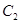 都相切.
都相切.
解析试题分析:.解:(1)因为抛物线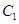 经过椭圆
经过椭圆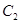 的两个焦点
的两个焦点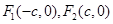 ,
,
所以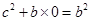 ,即
,即 ,由
,由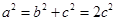 ,
,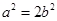
椭圆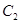 的方程为:
的方程为: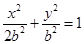 ,联立抛物线
,联立抛物线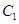 的方程
的方程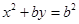
得: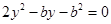 , 解得:
, 解得: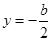 或
或 (舍去),所以
(舍去),所以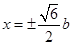 ,
,
即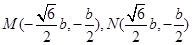 ,所以
,所以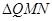 的重心坐标为
的重心坐标为 .
.
因为重心在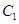 上,所以
上,所以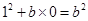 ,得
,得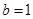 .所以
.所以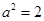 .
.
所以抛物线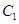 的方程为:
的方程为: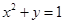 , 椭圆
, 椭圆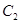 的方程为:
的方程为: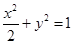 .
.
(2)因抛物线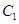 :
: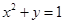 开口向下且关于y轴对称,所以与x轴垂直的直线都不是其切线。
开口向下且关于y轴对称,所以与x轴垂直的直线都不是其切线。
所以可设直线y=kx+m与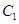 和
和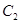 都相切,
都相切,
则由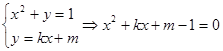 有相等实根
有相等实根 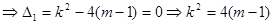
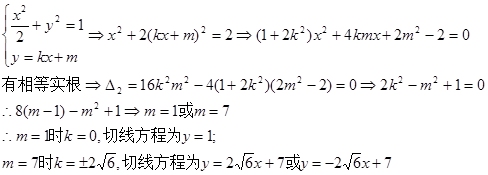
有3条直线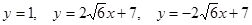 与
与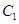 和
和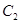 都相切.
都相切.
考点:抛物线和椭圆的方程的求解
点评:解决的关键是利用方程的性质得到a,bc的值,同时利用线圆相切的关系来分析结论,属于基础题。

练习册系列答案
相关题目
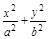 ="1" (a>b>0)的左、右焦点分别为F1、F2, F2也是抛物线C2:y2=4x的焦点,点M为C1与C2在第一象限的交点,且|MF2|=
="1" (a>b>0)的左、右焦点分别为F1、F2, F2也是抛物线C2:y2=4x的焦点,点M为C1与C2在第一象限的交点,且|MF2|=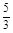 .
.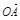 ·
·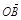 =0,求直线l的方程.
=0,求直线l的方程.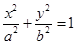 (a>b>0)的两个焦点和短轴的两个端点都在圆
(a>b>0)的两个焦点和短轴的两个端点都在圆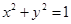 上.
上.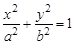
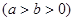 的一个顶点为B
的一个顶点为B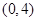 ,离心率
,离心率
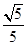 ,
,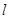 的方程.
的方程.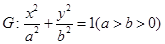 的离心率为
的离心率为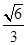 ,右焦点为(
,右焦点为(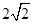 ,0),斜率为1的直线
,0),斜率为1的直线 与椭圆G交与A、B两点,以AB为底边作等腰三角形,顶点为
与椭圆G交与A、B两点,以AB为底边作等腰三角形,顶点为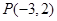 .
.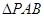 的面积.
的面积.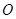 为极点,
为极点,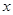 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线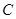 的极坐标方程是
的极坐标方程是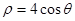 ,直线
,直线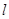 的参数方程是
的参数方程是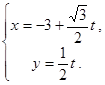 (
( 为参数)。
为参数)。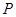 的极坐标;
的极坐标; 、
、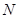 分别为曲线
分别为曲线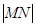 的最小值。
的最小值。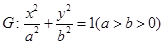 的离心率为
的离心率为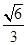 ,右焦点为
,右焦点为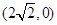 。斜率为1的直线
。斜率为1的直线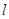 与椭圆
与椭圆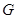 交于
交于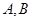 两点,以
两点,以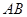 为底边作等腰三角形,顶点为
为底边作等腰三角形,顶点为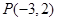 。
。 的面积。
的面积。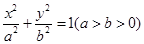 的左焦点为F,过点F的直线与椭圆C相交于A,B两点,直线l的倾斜角为60o,
的左焦点为F,过点F的直线与椭圆C相交于A,B两点,直线l的倾斜角为60o,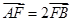 .
.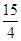 ,求椭圆C的方程.
,求椭圆C的方程. :
: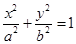
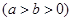 的两个焦点为
的两个焦点为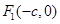 、
、 和顶点
和顶点 、
、 构成面积为32的正方形.
构成面积为32的正方形.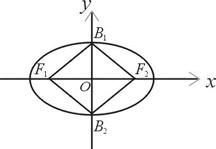
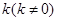 的直线
的直线 与椭圆
与椭圆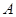 、
、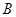 、
、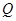 为
为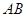 的中点,且
的中点,且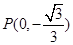 . 问:
. 问: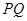 对称. 若能,求出
对称. 若能,求出 的取值范围;若不能,请说明理由.
的取值范围;若不能,请说明理由.