题目内容
圆(x-1)2+(y-1)2=4上到直线3x-4y+6=0的距离为2的点共有 个.
考点:直线与圆的位置关系
专题:直线与圆
分析:求出圆心(1,1)到直线3x-4y+6=0的距离d=
(r为半径),从而得出结论.
| r |
| 2 |
解答:
解:圆(x-1)2+(y-1)2=4的圆心(1,1)到直线3x-4y+6=0的距离d=
=1,
故有d=
(r为半径),
故圆(x-1)2+(y-1)2=4上到直线3x-4y+6=0的距离为2的点共有3个,
故答案为:3.
| |3-4+6| | ||
|
故有d=
| r |
| 2 |
故圆(x-1)2+(y-1)2=4上到直线3x-4y+6=0的距离为2的点共有3个,
故答案为:3.
点评:本题主要考查直线和圆的位置关系,点到直线的距离公式,属于中档题.

练习册系列答案
相关题目
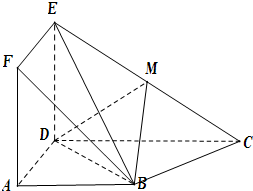 如图,正方形ADEF与梯形ABCD所在平面互相垂直,AD⊥CD,AB∥CD,AB=AD=
如图,正方形ADEF与梯形ABCD所在平面互相垂直,AD⊥CD,AB∥CD,AB=AD= 如图,在Rt△ABD中,∠BAD=
如图,在Rt△ABD中,∠BAD=