题目内容
20.若抛物线y2=4x与直线x-y-1=0交于 A,B两点,则|AB|=( )| A. | 2 | B. | 4 | C. | 6 | D. | 8 |
分析 联立方程组,消去y,利用韦达定理以及抛物线的性质能求出|AB|的值.
解答 解:抛物线的焦点坐标(1,0),直线x-y-1=0经过抛物线的焦点.
联立方程组$\left\{\begin{array}{l}x-y-1=0\\{y}^{2}=4x\end{array}\right.$,
得x2-6x+1=0,
设A(x1,y1),B(x2,y2),则x1+x2=6,x1•x2=-1,k=1,
∴|AB|=x1+x2+p=8.
故选:D.
点评 本题考查抛物线解得性质的应用,解题时要认真审题,注意转化思想的合理运用.

练习册系列答案
 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目
5.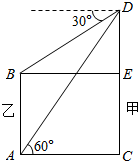 如图,甲、乙两楼相距20米,从乙楼底望甲楼顶的仰角为60°,从甲楼顶望乙楼顶的俯角为30°,则乙楼的高是( )
如图,甲、乙两楼相距20米,从乙楼底望甲楼顶的仰角为60°,从甲楼顶望乙楼顶的俯角为30°,则乙楼的高是( )
 如图,甲、乙两楼相距20米,从乙楼底望甲楼顶的仰角为60°,从甲楼顶望乙楼顶的俯角为30°,则乙楼的高是( )
如图,甲、乙两楼相距20米,从乙楼底望甲楼顶的仰角为60°,从甲楼顶望乙楼顶的俯角为30°,则乙楼的高是( )| A. | $\frac{40\sqrt{3}}{3}$ | B. | 20$\sqrt{3}$ | C. | 40 | D. | 10$\sqrt{2}$ |
9.“x<4”是“$\sqrt{x}$<2”的( )
| A. | 充分非必要条件 | B. | 必要非充分条件 | ||
| C. | 充要条件 | D. | 既非充分又非必要条件 |
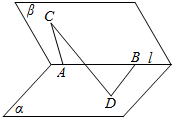 如图,在二面角α-l-β的棱l上有A,B两点,直线AC,BD分别在这个二面角的两个半平面内,且都垂直于AB,若二面角α-l-β的大小为$\frac{π}{3}$,AB=AC=2,CD=$\sqrt{11}$,则BD=3.
如图,在二面角α-l-β的棱l上有A,B两点,直线AC,BD分别在这个二面角的两个半平面内,且都垂直于AB,若二面角α-l-β的大小为$\frac{π}{3}$,AB=AC=2,CD=$\sqrt{11}$,则BD=3.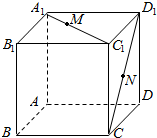 在长方体ABCD-A1B1C1D1中,|AB|=|AD|=3,|AA1|=3,点M在A1C1上,|MC1|=2|A1M|,N在D1C上且为D1C的中点,求M,N两点间的距离.
在长方体ABCD-A1B1C1D1中,|AB|=|AD|=3,|AA1|=3,点M在A1C1上,|MC1|=2|A1M|,N在D1C上且为D1C的中点,求M,N两点间的距离.