题目内容
8.设AB是双曲线Γ的实轴,点C在Γ上,且∠CAB=$\frac{π}{4}$,若AB=4,BC=$\sqrt{26}$,则双曲线的焦距是4$\sqrt{6}$.分析 在△ABC中,由余弦定理得CB2=CA2+BA2-2CABAcos$\frac{π}{4}$,解得CA=5$\sqrt{2}$,过C作CM⊥x轴于M,可得C,点C坐标代入双曲线方程得$\frac{9}{{2}^{2}}-\frac{25}{{b}^{2}}=1$,解得b2,c=$\sqrt{{a}^{2}+{b}^{2}}$即可.,
解答 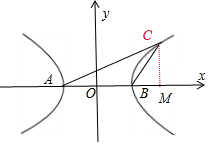 解:如图所示,在△ABC中,由余弦定理得CB2=CA2+BA2-2CABAcos$\frac{π}{4}$,解得CA=5$\sqrt{2}$,
解:如图所示,在△ABC中,由余弦定理得CB2=CA2+BA2-2CABAcos$\frac{π}{4}$,解得CA=5$\sqrt{2}$,
过C作CM⊥x轴于M,CM=5$\sqrt{2}$×$cos\frac{π}{4}$=5,AM=5$\sqrt{2}$,
∴C(3,5),点C坐标代入双曲线方程得$\frac{9}{{2}^{2}}-\frac{25}{{b}^{2}}=1$,解得b2=20,
c=$\sqrt{{a}^{2}+{b}^{2}}=2\sqrt{6}$,双曲线的焦距是2c=4$\sqrt{6}$.
故答案为:4$\sqrt{6}$.
点评 本题考查了直线与双曲线的位置关系,利用平面几何知识和圆锥曲线的定义是解此类题的有效方法,属于中档题.

练习册系列答案
 发散思维新课堂系列答案
发散思维新课堂系列答案
相关题目
17.已知f(x)是可导的函数,且f′(x)<f(x)对于x∈R恒成立,则( )
| A. | f(1)<ef(0),f(2017)>e2017f(0) | B. | f(1)>ef(0),f(2017)>e2017f(0) | ||
| C. | f(1)>ef(0),f(2017)<e2017f(0) | D. | f(1)<ef(0),f(2017)<e2017f(0) |
18.直线l将圆x2+y2-2x-4y=0平分,且与直线x+2y=0垂直,则直线l的方程是( )
| A. | 2x-y=0 | B. | 2x-y-2=0 | C. | x+2y-3=0 | D. | x-2y+3=0 |
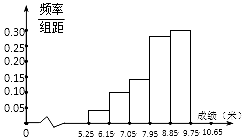 某校举行运动会,其中三级跳远的成绩在8.0米 (四舍五入,精确到0.1米) 以上的进入决赛,把所得数据进行整理后,分成6组画出频率分布直方图的一部分(如图),已知从左到右前5个小组的频率分别为0.04,0.10,0.14,0.28,0.30,第6小组的频数是7.
某校举行运动会,其中三级跳远的成绩在8.0米 (四舍五入,精确到0.1米) 以上的进入决赛,把所得数据进行整理后,分成6组画出频率分布直方图的一部分(如图),已知从左到右前5个小组的频率分别为0.04,0.10,0.14,0.28,0.30,第6小组的频数是7.