题目内容
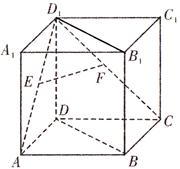
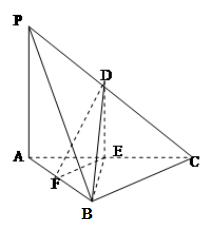
如图,在正方体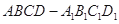 中,
中,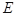 、
、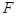 分别为
分别为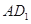 ,
,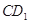 中点。
中点。
(1)求异面直线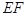 与
与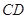 所成角的大小;
所成角的大小;
(2)求证: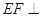 平面
平面 。
。
 中,
中, 、
、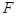 分别为
分别为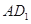 ,
,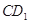 中点。
中点。(1)求异面直线
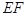 与
与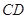 所成角的大小;
所成角的大小;(2)求证:
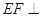 平面
平面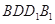 。
。
(1) ;(2)见试题解析
;(2)见试题解析
 ;(2)见试题解析
;(2)见试题解析试题分析:(1)把异面直线通过平移到一个平面内,即可求异面直线所成角。(2)由线面垂直的判定定理得,要证明
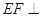 平面
平面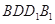 ,只需证明
,只需证明 垂直于平面
垂直于平面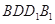 内的两条相交直线,因为
内的两条相交直线,因为 ,
, ,
, 得
得 ,又
,又 平面
平面 ,且
,且 ,所以
,所以 平面
平面
试题解析:(1)解: 连结
 。如图所示:
。如图所示:


 、
、 分别为
分别为 ,
, 中点。
中点。

 异面直线
异面直线 与
与 所成角即为
所成角即为 。(2分)
。(2分)在等腰直角
 中
中
故异面直线
 与
与 所成角的大小为
所成角的大小为 。(4分)
。(4分)(2)证明:在正方形中


 (6分)
(6分)又

 平面
平面 (8分)
(8分)
练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案
相关题目
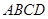 中,
中,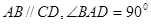 ,
,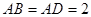 ,
,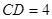 ,点
,点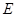 为线段
为线段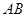 上异于
上异于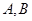 的点,且
的点,且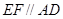 ,沿
,沿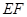 将面
将面 折起,使平面
折起,使平面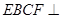 平面
平面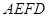 ,如图2.
,如图2.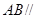 平面
平面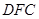 ;
;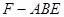 体积最大时,求平面
体积最大时,求平面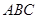 与平面
与平面
 中,
中, 分别为棱
分别为棱 的中点,已知
的中点,已知 ,
,
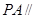 平面
平面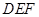 ;
;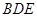
 平面
平面 .
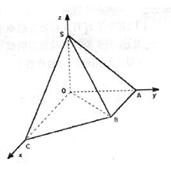
.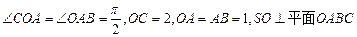 ,SO=1,以OC、OA、OS分别为x轴、y轴、z轴建立直角坐标系O-xyz.
,SO=1,以OC、OA、OS分别为x轴、y轴、z轴建立直角坐标系O-xyz.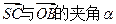 的大小(用反三角函数表示);
的大小(用反三角函数表示);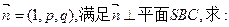
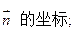
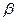 (用反三角函数表示);
(用反三角函数表示);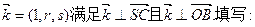
 .
. 
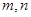 是不同的直线,
是不同的直线,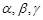 是不同的平面,有以下四个命题:
是不同的平面,有以下四个命题: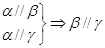 ②
②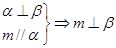
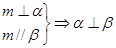 ④
④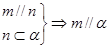
 平面
平面 ,直线
,直线
 平面
平面 ,给出下列命题,其中正确的是( )
,给出下列命题,其中正确的是( ) ②
②
 ④
④
 类比此性质,如下图,在四面体P-ABC中,若PA、PB、PC两两垂直,底面ABC上的高为h,则得到的正确结论为__________________________.
类比此性质,如下图,在四面体P-ABC中,若PA、PB、PC两两垂直,底面ABC上的高为h,则得到的正确结论为__________________________.