题目内容
 如图,梯形ABCD内接于⊙O,AD∥BC,过点B引⊙O的切线分别交DA、CA的延长线于E、F,已知BC=8,CD=5,AF=6,则EF=________.
如图,梯形ABCD内接于⊙O,AD∥BC,过点B引⊙O的切线分别交DA、CA的延长线于E、F,已知BC=8,CD=5,AF=6,则EF=________.

分析:根据两个角对应相等,写出两个三角形相似,得到对应边成比例,得到AE的长,再根据三角形相似,得到FB的长,最后根据切割线定理,得到要求的结果.
解答:
 ∵梯形ABCD内接于⊙O,AD∥BC,
∵梯形ABCD内接于⊙O,AD∥BC,∴梯形是等腰梯形,又CD=5
∴AB=DC=5,
又BF是切线,
∴∠ABF=∠ACB,∠EAB=∠DCB=∠ABC
∴△ABE∽△BCA,
∴AB2=AE•BC,
∴AE=
 ,
,又由DA∥BC,可得出△FEA∽△FBC,
∴

∴FC=
 ,
,∵FB2=FA•FC
∴FB=
 ,
,又由△ABE∽△BCA可得出BE=
 =
=
∴EF=

故答案为:

点评:本题考查与圆有关的比例线段,是一个多次使用三角形相似来证明线段成比例的题目,注意在解题时观察题目中要用的线段,看清题目的发展方向.

练习册系列答案
相关题目
 如图,梯形ABCD内接于⊙O,AD∥BC,过点C作⊙O的切线,交BD的延长线于点P,交AD的延长线于点E.
如图,梯形ABCD内接于⊙O,AD∥BC,过点C作⊙O的切线,交BD的延长线于点P,交AD的延长线于点E.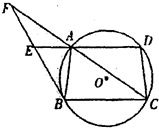 如图,梯形ABCD内接于⊙O,AD∥BC,过点B引⊙O的切线分别交DA、CA的延长线于E、F,已知BC=8,CD=5,AF=6,则EF=
如图,梯形ABCD内接于⊙O,AD∥BC,过点B引⊙O的切线分别交DA、CA的延长线于E、F,已知BC=8,CD=5,AF=6,则EF= 如图,梯形ABCD内接于⊙O,AB∥CD,AB为直径,DO平分∠ADC,则∠DAO的度数是
如图,梯形ABCD内接于⊙O,AB∥CD,AB为直径,DO平分∠ADC,则∠DAO的度数是
 【选修4-1:几何证明选讲】
【选修4-1:几何证明选讲】