题目内容
如图，梯形ABCD内接于⊙O，AD∥BC，过点C作⊙O的切线，交BD的延长线于点P，交AD的延长线于点E。
（1）求证：AB2=DE·BC；
（2）若BD=9，AB=6，BC=9，求切线PC的长。
（2）若BD=9，AB=6，BC=9，求切线PC的长。
解：（1）∵AD∥BC，
∴AB=CD，∠EDC=∠BCD，
又PC与⊙O相切
∴∠ECD=∠DBC，
∴△CDE∽△BCD ，
∴
∴CD2=DE·BC，即AB2=DE·BC。
（2）由（1）知，DE=
∵△PDE∽△PBC，
∴
又∵PB-PD=9，
∴
∴
∴
。
∴AB=CD，∠EDC=∠BCD，
又PC与⊙O相切
∴∠ECD=∠DBC，
∴△CDE∽△BCD ，
∴
∴CD2=DE·BC，即AB2=DE·BC。
（2）由（1）知，DE=
∵△PDE∽△PBC，
∴
又∵PB-PD=9，
∴
∴
∴
。
练习册系列答案
相关题目
如图，梯形ABCD内接于⊙O，AD∥BC，过点C作⊙O的切线，交BD的延长线于点P，交AD的延长线于点E．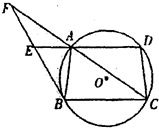
如图，梯形ABCD内接于⊙O，AD∥BC，过点B引⊙O的切线分别交DA、CA的延长线于E、F，已知BC=8，CD=5，AF=6，则EF=
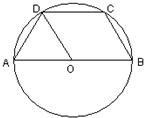如图，梯形ABCD内接于⊙O，AB∥CD，AB为直径，DO平分∠ADC，则∠DAO的度数是
【选修4-1：几何证明选讲】