题目内容
10.已知a>0且a≠1,函数k(x)=loga(x+1),f(x)=loga(x+1),g(x)=loga$\frac{1}{1-x}$,记F(x)=2k(x)+g(x).(1)求函数F(x)的定义域D及其零点;
(2)若关于x的方程F(x)-m=0在区间[0,1)内仅有一解,求实数m的取值范围.
分析 (1)先根据对数函数的图象和性质确定函数的定义域,再根据对数的运算性质得出方程(x+1)2=1-x,解出方程检验即可;
(1)先分离参数m得到${a^m}=1-x+\frac{4}{1-x}-4$,再根据函数的单调性确定参数m的取值范围.
解答 解:(1)F(x)=2k(x)+g(x)=$2{log_a}(x+1)+{log_a}\frac{1}{1-x}$(a>0且a≠1),
要使函数式有意义,则$\left\{\begin{array}{l}x+1>0\\ 1-x>0\end{array}\right.$,解得-1<x<1,
所以函数F(x)的定义域为:D=(-1,1),
令F(x)=0,则$2{log_a}(x+1)+{log_a}\frac{1}{1-x}=0$,------(*)
方程变为:${log_a}{(x+1)^2}={log_a}(1-x)$,即(x+1)2=1-x,
整理得,x2+3x=0,解得x1=0,x2=-3,
经检验方程(*)的解为x=0,x=-3不合题意,
所以函数F(x)的零点为0;
(2)原方程可写成:$m=2{log_a}(x+1)+{log_a}\frac{1}{1-x}$(0≤x<1),
m=${log_a}\frac{{{x^2}+2x+1}}{1-x}={log_a}(1-x+\frac{4}{1-x}-4)$,
即${a^m}=1-x+\frac{4}{1-x}-4$,
设1-x=t∈(0,1],因为函数$y=t+\frac{4}{t}$在区间(0,1]上是减函数,
所以,当t=1时,此时x=0,ymin=5,因此,am≥1,
①当a>1时,由am≥1解得,m≥0,
且y=ax为增函数,因此,m≥0时,原方程在区间[0,1)内仅有一解;
②当0<a<1时,由am≥1解得,m≤0,
且y=ax为减函数,因此,m≤0时,原方程在区间[0,1)内仅有一解.
点评 本题主要考查了对数函数的图象和性质,涉及函数定义域的确定和函数零点的求解,以及运用双勾函数的性质分析函数零点的个数,属于中档题.

| A. | 向右平移$\frac{π}{12}$个单位 | B. | 向左平移$\frac{π}{12}$个单位 | ||
| C. | 向右平移$\frac{π}{3}$个单位 | D. | 向左平移$\frac{π}{3}$个单位 |
| A. | 最小正周期为$\frac{π}{2}$的奇函数 | B. | 最小正周期为π的奇函数 | ||
| C. | 最小正周期为π的偶函数 | D. | 最小正周期为2π的偶函数 |
| A. | b<c<a | B. | b<a<c | C. | a<b<c | D. | c<a<b |
| A. | 4$\overrightarrow{a}$-2$\overrightarrow{b}$ | B. | 4$\overrightarrow{a}$+2$\overrightarrow{b}$ | C. | -2$\overrightarrow{a}$+4$\overrightarrow{b}$ | D. | 2$\overrightarrow{a}$+4$\overrightarrow{b}$ |
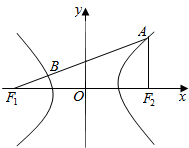 已知双曲线中心在原点,焦点在x轴上,过左焦点F1作倾斜角为30°的直线l,交双曲线于A,B两点,F2为双曲线的右焦点,且AF2⊥x轴,如图.
已知双曲线中心在原点,焦点在x轴上,过左焦点F1作倾斜角为30°的直线l,交双曲线于A,B两点,F2为双曲线的右焦点,且AF2⊥x轴,如图.