题目内容
如图,棱锥P—ABCD的底面ABCD是矩形,PA⊥平面ABCD,PA=AD=2,BD=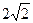 .
.
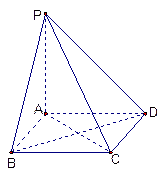
(Ⅰ)求证:BD⊥平面PAC;
(Ⅱ)求二面角P—CD—B的大小;
(Ⅲ)求点C到平面PBD的距离.
 .
.
(Ⅰ)求证:BD⊥平面PAC;
(Ⅱ)求二面角P—CD—B的大小;
(Ⅲ)求点C到平面PBD的距离.
(1)略
(2)q = 450
(3)
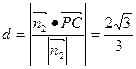
解:(Ⅱ)由(Ⅰ)得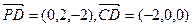 .
.
设平面PCD的法向量为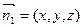 ,则
,则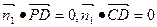 ,
,
即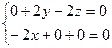 ,∴
,∴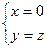 故平面PCD的法向量可取为
故平面PCD的法向量可取为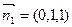
∵PA⊥平面ABCD,∴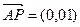 为平面ABCD的法向量.
为平面ABCD的法向量.
设二面角P—CD—B的大小为q,依题意可得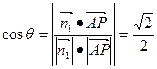 ,∴q = 450 .
,∴q = 450 .
(Ⅲ)由(Ⅰ)得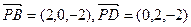 ,设平面PBD的法向量为
,设平面PBD的法向量为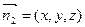 ,
,
则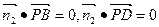 ,即
,即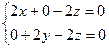 ,∴x=y=z,
,∴x=y=z,
故平面PBD的法向量可取为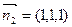 .
.
∵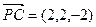 ,∴C到面PBD的距离为
,∴C到面PBD的距离为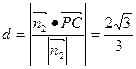
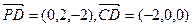 .
. 设平面PCD的法向量为
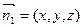 ,则
,则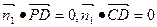 ,
,即
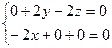 ,∴
,∴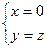 故平面PCD的法向量可取为
故平面PCD的法向量可取为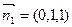
∵PA⊥平面ABCD,∴
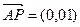 为平面ABCD的法向量.
为平面ABCD的法向量. 设二面角P—CD—B的大小为q,依题意可得
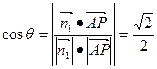 ,∴q = 450 .
,∴q = 450 . (Ⅲ)由(Ⅰ)得
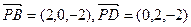 ,设平面PBD的法向量为
,设平面PBD的法向量为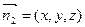 ,
,则
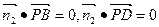 ,即
,即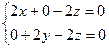 ,∴x=y=z,
,∴x=y=z,故平面PBD的法向量可取为
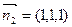 .
. ∵
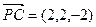 ,∴C到面PBD的距离为
,∴C到面PBD的距离为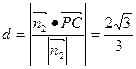

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 目标测试系列答案
目标测试系列答案
相关题目
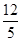
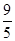
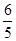
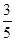
 ,BC=4,
,BC=4,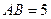 ,AA1=4,点D是AB的中点.
,AA1=4,点D是AB的中点.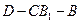 的余弦值.
的余弦值.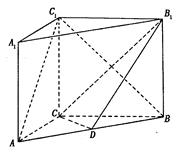
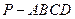 中,侧棱
中,侧棱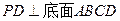 ,底面
,底面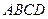 是直角梯形,
是直角梯形,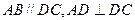 ,且
,且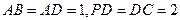 ,
,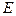 是
是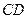 的中点
的中点 .
.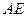 与
与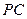 所成的角;
所成的角;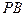
 上是否存在一点
上是否存在一点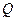 ,使得
,使得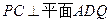 ?若存在,求出
?若存在,求出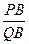 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.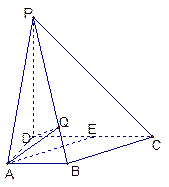

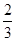

 的菱形,∠ACC1为锐角,侧面ABB1A1⊥侧面AA
的菱形,∠ACC1为锐角,侧面ABB1A1⊥侧面AA 1C1C,且A1B=AB=AC=1.
1C1C,且A1B=AB=AC=1.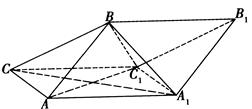
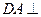 平面ABC,
平面ABC,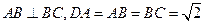 ,则球O的体积等于 。
,则球O的体积等于 。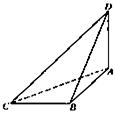
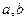 和平面
和平面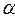 ,且
,且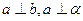 ,则
,则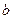 与
与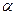 的位置关系是______________
的位置关系是______________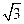 ,
,