题目内容
下列命题中,错误的是( )
| A、一条直线与两个平行平面中的一个相交,则必与另一个面相交 |
| B、平行于同一平面的两条直线不一定平行 |
| C、如果平面α不垂直于平面β,那么平面α内一定不存在直线垂直于平面 |
| D、若直线l不平行于平面α内不存在与l平行的直线 |
考点:空间中直线与平面之间的位置关系
专题:常规题型,作图题,空间位置关系与距离
分析:选项A可利用反证法证明,
选项B可在正方体中找到;
选项C是线面垂直判定定理的逆否命题;
选项D可以举反例即可,直线l可能在平面α内.
选项B可在正方体中找到;
选项C是线面垂直判定定理的逆否命题;
选项D可以举反例即可,直线l可能在平面α内.
解答:
 解:选项A:一条直线与两个平行平面中的一个相交,则必与另一个面相交,正确;
解:选项A:一条直线与两个平行平面中的一个相交,则必与另一个面相交,正确;
反证法:假设a∥α或a?α内,
则由α∥β可知,
a∥β或a?β,
与a∩β=A相矛盾,
故假设不成立;
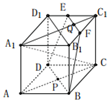
选项B:平行于同一平面的两条直线不一定平行,正确,例如正方体中的A1B1与B1C1都与平面ABCD平行,但它们相交;选项C:如果平面α不垂直于平面β,那么平面α内一定不存在直线垂直于平面,正确,
是线面垂直判定定理的逆否命题;
选项D:若直线l不平行于平面α,则α内不存在与l平行的直线,不正确,
直线l不平行于平面α,则直线l可能在平面α内,
很容易作出直线与直线l平行.
故选D.
 解:选项A:一条直线与两个平行平面中的一个相交,则必与另一个面相交,正确;
解:选项A:一条直线与两个平行平面中的一个相交,则必与另一个面相交,正确;反证法:假设a∥α或a?α内,
则由α∥β可知,
a∥β或a?β,
与a∩β=A相矛盾,
故假设不成立;
选项B:平行于同一平面的两条直线不一定平行,正确,例如正方体中的A1B1与B1C1都与平面ABCD平行,但它们相交;选项C:如果平面α不垂直于平面β,那么平面α内一定不存在直线垂直于平面,正确,
是线面垂直判定定理的逆否命题;
选项D:若直线l不平行于平面α,则α内不存在与l平行的直线,不正确,
直线l不平行于平面α,则直线l可能在平面α内,
很容易作出直线与直线l平行.
故选D.
点评:本题考查了线面的位置关系的判断及应用,属于中档题.

练习册系列答案
相关题目
已知函数y=f(x-1)的定义域为[1,3],则函数y=f(log3x)的定义域为( )
| A、[1,9] |
| B、[0,1] |
| C、[0,2] |
| D、[0,9] |
已知椭圆C的方程为
+
=1,设M(x1,y1)、N(x2,y2)为椭圆C上不同的点,直线MN的斜率为k1,A点满足
+
=λ
(λ≠0)的点,且直线OA的斜率为k2,求k1+k2的值.
| x2 |
| 4 |
| y2 |
| 3 |
| OM |
| ON |
| OA |
已知椭圆的一个焦点为F(0,1),离心率e=
,则该椭圆的标准程为( )
| 1 |
| 2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、x2+
|
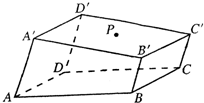 如图所示的一块木料中,棱BC平行于面A′C′.
如图所示的一块木料中,棱BC平行于面A′C′.