题目内容
已知椭圆C的方程为
+
=1,设M(x1,y1)、N(x2,y2)为椭圆C上不同的点,直线MN的斜率为k1,A点满足
+
=λ
(λ≠0)的点,且直线OA的斜率为k2,求k1+k2的值.
| x2 |
| 4 |
| y2 |
| 3 |
| OM |
| ON |
| OA |
考点:椭圆的应用
专题:计算题,圆锥曲线的定义、性质与方程
分析:由题意,
=(x1,y1),
=(x2,y2),又由
+
=λ
(λ≠0),k1=
,k2=
,化简可得k1+k2=-
.
| OM |
| ON |
| OM |
| ON |
| OA |
| y2-y1 |
| x2-x1 |
| y1+y2 |
| x1+x2 |
| 3 |
| sinβcosβ-sinacosa |
| cos2a-cos2β |
解答:
解:由题意,
=(x1,y1),
=(x2,y2);
∵
+
=λ
(λ≠0),
∴
=
(
+
)
=
(x1+x2,y1+y2),
∴k1=
,k2=
,
∴k1+k2=
+
=
[(y2-y1)(x1+x2)+(y2+y1)(x2-x1)]
=2
(y2x2-y1x1)
设x1=2cosa,y1=
sina,x2=2cosβ,y2=
sinβ,
则2
(y2x2-y1x1)
=-
.
| OM |
| ON |
∵
| OM |
| ON |
| OA |
∴
| OA |
| 1 |
| λ |
| OM |
| ON |
=
| 1 |
| λ |
∴k1=
| y2-y1 |
| x2-x1 |
| y1+y2 |
| x1+x2 |
∴k1+k2=
| y2-y1 |
| x2-x1 |
| y1+y2 |
| x1+x2 |
=
| 1 |
| (x2-x1)(x2+x1) |
=2
| 1 |
| (x2-x1)(x2+x1) |
设x1=2cosa,y1=
| 3 |
| 3 |
则2
| 1 |
| (x2-x1)(x2+x1) |
=-
| 3 |
| sinβcosβ-sinacosa |
| cos2a-cos2β |
点评:本题考查了圆锥曲线与直线的位置关系,同时考查了直线的斜率,属于中档题.

练习册系列答案
 金钥匙试卷系列答案
金钥匙试卷系列答案
相关题目
下列命题中,错误的是( )
| A、一条直线与两个平行平面中的一个相交,则必与另一个面相交 |
| B、平行于同一平面的两条直线不一定平行 |
| C、如果平面α不垂直于平面β,那么平面α内一定不存在直线垂直于平面 |
| D、若直线l不平行于平面α内不存在与l平行的直线 |
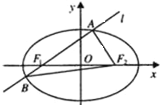 如图,椭圆
如图,椭圆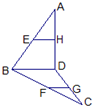 在空间四边形ABCD中,如图所示.
在空间四边形ABCD中,如图所示.