题目内容
3.下列命题,其中正确的是①(填写序号).①若m⊥α,m∥n,则n⊥α;
②若m∥n,m?α,n?β,则α∥β;
③若直线m∥n,则直线m就平行于平面α内的无数条直线;
④若∠ABC和∠A1B1C1的边AB∥A1B1,AC∥A1C1,则∠ABC=∠A1B1C1.
分析 在①中,由线面垂直的性质得n⊥α在②中,α与β相交或平行;在③中,直线m与平面α有可能相交;在④中,∠ABC=∠A1B1C1或∠ABC和∠A1B1C1互补.
解答 解:①若m⊥α,m∥n,则由线面垂直的性质得n⊥α,故①正确;
②若m∥n,m?α,n?β,则α与β相交或平行,故②错误;
③若直线m∥n,则直线m与平面α有可能相交,故③错误;
④若∠ABC和∠A1B1C1的边AB∥A1B1,AC∥A1C1,
则∠ABC=∠A1B1C1或∠ABC和∠A1B1C1互补,故④错误.
故答案为:①.
点评 本题考查命题真假的判断,是中档题,解题时要认真审题,注意空间中线线、线面、面面间的位置关系的合理运用.

练习册系列答案
相关题目
13.若实数x,y满足约束条件$\left\{\begin{array}{l}{3x-y-1≤0}\\{x-y≥0}\\{2x+y≥0}\end{array}\right.$,则目标函数z=x+y的最大值为( )
| A. | 2 | B. | 1 | C. | -1 | D. | -2 |
11.已知一个平面α,那么对于空间内的任意一条直线l,在平面α内一定存在一条直线m,使得直线l与直线m( )
| A. | 平行 | B. | 相交 | C. | 异面 | D. | 垂直 |
18.若曲线y2=2px(p>0)上只有一个点到其焦点的距离为1,则p的值为( )
| A. | 4 | B. | 3 | C. | 2 | D. | 1 |
8.设集合A={2,5},集合B={1,2},集合C={1,2,5,7},则(A∪B)∩C为( )
| A. | {1,2,5} | B. | {2,5} | C. | {2,5,7} | D. | {1,2,5,7} |
15.已知集合M={1,2,3},N={2,3,4,5},那么M∩N=( )
| A. | ∅ | B. | {1,4,5} | C. | {1,2,3,4,5} | D. | {2,3} |
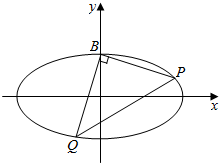 如图,已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的离心率是$\frac{{\sqrt{3}}}{2}$,一个顶点是B(0,1).
如图,已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的离心率是$\frac{{\sqrt{3}}}{2}$,一个顶点是B(0,1).