Question

【题目】已知椭圆的左右两焦点分别为、.

（1）若矩形的边在轴上，点、均在上，求该矩形绕轴旋转一周所得圆柱侧面积的取值范围；

（2）设斜率为的直线与交于、两点，线段的中点为（），求证：；

（3）过上一动点作直线，其中，过作直线的垂线交轴于点，问是否存在实数，使得恒成立，若存在，求出的值，若不存在，说明理由.

Answer 1

【答案】（1）；（2）见解析；（3）1.

【解析】

（1）设D（x，y），由D在椭圆上，可得|xy|，再由矩形绕y轴旋转一周后所得圆柱体侧面积为S侧＝2π|BC||AB|＝4π|xy|求解；

（2）设P（x1，y1），Q（x2，y2），利用点差法可得k，再由M（1，m）在椭圆内部，得m2，即0＜m，由此证明结论；

（3）直线的斜率为，则，求出，，再由到角公式可得ER为∠F1EF2的角分线，得到，即|EF1||RF2|＝λ|EF2||RF1|，可知存在实数λ＝1，使得|EF1||RF2|＝λ|EF2||RF1|恒成立．

（1）解：设D（x，y），由D在椭圆上，

得1，得|xy|，

当且仅当，即，时取“＝”．

矩形绕y轴旋转一周后所得圆柱体侧面积为S侧＝2π|BC|AB|＝4π|xy|，

∴S侧＝4π|xy|≤4π；

（2）证明：设P（x1，y1），Q（x2，y2），

则，，

两式作差可得：k，

由M（1，m）在椭圆内部，得，即m2，

又m＞0，∴0＜m，得k；

（3）解：直线的斜率为，则，

又，，

设直线EF1到直线ER的角为α，直线ER到直线EF2的角为β，

则tanα，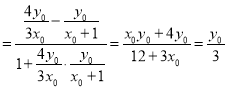

tanβ．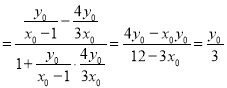

∴tanα＝tanβ，则α＝β，即ER为∠F1EF2的角分线，

∴，即|EF1||RF2|＝λ|EF2||RF1|，

∴存在实数λ＝1，使得|EF1||RF2|＝λ|EF2||RF1|恒成立．