题目内容
10.已知向量$\overrightarrow{a}$=(x,2),$\overrightarrow{b}$=(2,1),$\overrightarrow{c}$=(3,x),若$\overrightarrow{a}$∥$\overrightarrow{b}$,则$\overrightarrow{a}$•$\overrightarrow{c}$=( )| A. | 4 | B. | 8 | C. | 12 | D. | 20 |
分析 根据题意,由于$\overrightarrow{a}$∥$\overrightarrow{b}$,结合向量的坐标运算可得x=2×2=4,即可得向量$\overrightarrow{a}$、$\overrightarrow{c}$的坐标,计算可得$\overrightarrow{a}$•$\overrightarrow{c}$的值,即可得答案.
解答 解:根据题意,向量$\overrightarrow{a}$=(x,2),$\overrightarrow{b}$=(2,1),
若$\overrightarrow{a}$∥$\overrightarrow{b}$,则有x=2×2=4,
即$\overrightarrow{a}$=(4,2),$\overrightarrow{c}$=(3,4),则$\overrightarrow{a}$•$\overrightarrow{c}$=4×3+2×4=20;
故选:D.
点评 本题考查向量数量积的运算,涉及向量的坐标计算,关键是求出x的值.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
20.设全集U=R+,集合A={x|log0.5x≥-1},B={x||x|>1},则“x∈A”是“x∈∁UB”的( )
| A. | 充分条件 | B. | 必要条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
1.函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图,f($\frac{π}{2}$)=-1,则f(0)的值为( )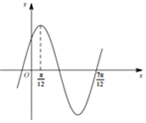

| A. | 1 | B. | $\frac{1}{2}$ | C. | $\sqrt{2}$ | D. | $\frac{\sqrt{2}}{2}$ |
18.在△ABC中,BC=1且cosA=-$\frac{\sqrt{10}}{10}$,B=$\frac{π}{4}$,则BC边上的高等于( )
| A. | 1 | B. | $\frac{1}{2}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{4}$ |
5.学校某文具商店经营某种文具,商店每销售一件该文具可获利3元,若供大于求则削价处理,每处理一件文具亏损1元;若供不应求,则可以从外部调剂供应,此时每件文具仅获利2元.为了了解市场需求的情况,经销商统计了去年一年(52周)的销售情况.
以去年每周的销售量的频率为今年每周市场需求量的概率.
(1)要使进货量不超过市场需求量的概率大于0.5,问进货量的最大值是多少?
(2)如果今年的周进货量为14,写出周利润Y的分布列;
(3)如果以周利润的期望值为考虑问题的依据,今年的周进货量定为多少合适?
| 销售量(件) | 10 | 11 | 12 | 13 | 14 | 15 | 16 |
| 周数 | 2 | 4 | 8 | 13 | 13 | 8 | 4 |
(1)要使进货量不超过市场需求量的概率大于0.5,问进货量的最大值是多少?
(2)如果今年的周进货量为14,写出周利润Y的分布列;
(3)如果以周利润的期望值为考虑问题的依据,今年的周进货量定为多少合适?
15.已知数列{an}的各项均为正整数,其前n项和为Sn,an+1=$\left\{\begin{array}{l}{\frac{{a}_{n}+1}{2}{,a}_{n}是奇数}\\{{3a}_{n}-1{,a}_{n}是偶数}\end{array}\right.$,若S3=10,则S180=( )
| A. | 600或900 | B. | 900或560 | C. | 900 | D. | 600 |
8.已知函数f(x-1)=x2-2x,且f(a)=3,则实数a的值等于( )
| A. | $\sqrt{2}$ | B. | $±\sqrt{2}$ | C. | 2 | D. | ±2 |
9.下表提供了某厂节能降耗技术改造后,生产甲产品过程中记录的产量x(吨)与相应的生产能耗y(吨标准煤)的几组对照数据:
(1)请根据上表提供的数据,求出y关于x的回归直线方程;
(2)已知该厂技改前100吨甲产品的生产能耗为90吨标准煤.试根据(2)求出的回归直线方程,预测生产100吨甲产品的生产能耗比技改前降低多少吨标准煤?
附:$\widehat{b}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}$,a=$\overline{y}$-$\widehat{b}$$\overline{x}$.
| x | 3 | 4 | 5 | 6 | 7 |
| y | 2.5 | 3 | 4 | 4.5 | 6 |
(2)已知该厂技改前100吨甲产品的生产能耗为90吨标准煤.试根据(2)求出的回归直线方程,预测生产100吨甲产品的生产能耗比技改前降低多少吨标准煤?
附:$\widehat{b}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}$,a=$\overline{y}$-$\widehat{b}$$\overline{x}$.