题目内容
8.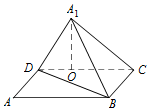 如图,已知矩形ABCD中,AB=10,BC=6,将矩形沿对角线BD把△ABD折起,使A移到A1点,且A1在平面BCD上的射影O恰在CD上,即A1O⊥平面DBC.
如图,已知矩形ABCD中,AB=10,BC=6,将矩形沿对角线BD把△ABD折起,使A移到A1点,且A1在平面BCD上的射影O恰在CD上,即A1O⊥平面DBC.(Ⅰ)求证:BC⊥A1D;
(Ⅱ)求证:平面A1BC⊥平面A1BD;
(Ⅲ)求点C到平面A1BD的距离.
分析 (Ⅰ)由线面垂直得A1O⊥BC,再由BC⊥DC,能证明BC⊥A1D.
(Ⅱ)由BC⊥A1D,A1D⊥A1B,得A1D⊥平面A1BC,由此能证明平面A1BC⊥平面A1BD.
(III)由${V}_{C-{A}_{1}BD}$=${V}_{{A}_{1}-DBC}$,能求出点C到平面A1BD的距离.
解答 证明:(Ⅰ)∵A1O⊥平面DBC,∴A1O⊥BC,
又∵BC⊥DC,A1O∩DC=O,
∴BC⊥平面A1DC,∴BC⊥A1D.
(Ⅱ)∵BC⊥A1D,A1D⊥A1B,BC∩A1B=B,
∴A1D⊥平面A1BC,
又∵A1D?平面A1BD,
∴平面A1BC⊥平面A1BD.
解:(III)设C到平面A1BD的距离为h,
∵${V}_{C-{A}_{1}BD}$=${V}_{{A}_{1}-DBC}$,
∴$\frac{1}{3}{S}_{△{A}_{1}BD}•h$=$\frac{1}{3}{S}_{△DBC}•{A}_{1}O$,
又∵${S}_{△{A}_{1}BD}$=S△DBC,${A}_{1}O=\frac{6×8}{10}=\frac{24}{5}$,∴$h=\frac{24}{5}$.
∴点C到平面A1BD的距离为$\frac{24}{5}$.
点评 本题考查异面直线垂直的证明,考查面面垂直的证明,考查点到平面的距离的求法,是中档题,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
相关题目
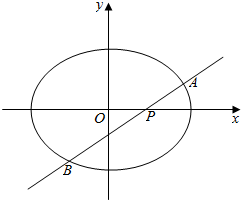 椭圆E:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)经过点(1,$\frac{\sqrt{2}}{2}$),且离心率为$\frac{\sqrt{2}}{2}$,过点P的动直线l与椭圆相交于A,B两点.
椭圆E:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)经过点(1,$\frac{\sqrt{2}}{2}$),且离心率为$\frac{\sqrt{2}}{2}$,过点P的动直线l与椭圆相交于A,B两点.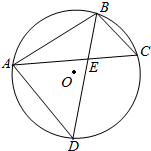 如图,圆O为△ABC的外接圆,D为$\widehat{AC}$的中点,BD交AC于E.
如图,圆O为△ABC的外接圆,D为$\widehat{AC}$的中点,BD交AC于E.