题目内容
【题目】选修4-4:坐标系与参数方程
在直角坐标系![]() 中,直线
中,直线![]() 经过点
经过点![]() ,其倾斜角为
,其倾斜角为![]() ,在以原点
,在以原点![]() 为极点,
为极点,![]() 轴非负半轴为极轴的极坐标系中(取相同的长度单位),曲线
轴非负半轴为极轴的极坐标系中(取相同的长度单位),曲线![]() 的极坐标方程为
的极坐标方程为![]()
(Ⅰ)若直线![]() 与曲线
与曲线![]() 有公共点,求
有公共点,求![]() 的取值范围;
的取值范围;
(Ⅱ)设![]() 为曲线
为曲线![]() 上任意一点,求
上任意一点,求![]() 的取值范围.
的取值范围.
【答案】(Ⅰ)![]() (Ⅱ)
(Ⅱ)![]()
【解析】
试题分析:(Ⅰ)由直线l经过点P(﹣1,0),且倾斜角为α,可得直线l的参数方程,利用互化公式可得C的直角坐标方程.由直线l与曲线C有公共点,可得![]() ,解出即可得出的取值范围;
,解出即可得出的取值范围;
(Ⅱ)设M(x,y)为曲线C上任意一点,利用参数方程为![]() (θ为参数),结合三角函数知识求
(θ为参数),结合三角函数知识求![]() 的取值范围.
的取值范围.
试题解析:
(Ⅰ)![]() 曲线
曲线![]() 的极坐标方程为
的极坐标方程为![]() ,
,
![]() 曲线
曲线![]() 的直角坐标方程为
的直角坐标方程为![]() ,
,
![]() 直线
直线![]() 经过点
经过点![]() ,其倾斜角为
,其倾斜角为![]() ,
,![]() 直线
直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),
为参数),
将![]() ,代入
,代入![]() 整理得
整理得![]() ,
,
![]() 直线
直线![]() 与曲线
与曲线![]() 有公共点,
有公共点,![]() 即
即![]() ,
,
![]() 的取值范围是
的取值范围是![]()
(Ⅱ)曲线![]() 的直角坐标方程为
的直角坐标方程为![]() 可化为
可化为![]() ,
,
其参数方程为![]() (
(![]() 为参数),
为参数),
![]() 为曲线
为曲线![]() 上任意一点,
上任意一点,
![]() ,其中
,其中![]() ,
,
![]() 的取值范围是
的取值范围是![]()

练习册系列答案
相关题目
【题目】某高三理科班共有![]() 名同学参加某次考试,从中随机挑出
名同学参加某次考试,从中随机挑出![]() 名同学,他们的数学成绩
名同学,他们的数学成绩![]() 与物理成绩
与物理成绩![]() 如下表:
如下表:
数学成绩 |
|
|
|
|
|
物理成绩 |
|
|
|
|
|
(1)数据表明![]() 与
与![]() 之间有较强的线性关系,求
之间有较强的线性关系,求![]() 关于
关于![]() 的线性回归方程;
的线性回归方程;
(2)本次考试中,规定数学成绩达到![]() 分为优秀,物理成绩达到
分为优秀,物理成绩达到![]() 分为优秀.若该班数学优秀率与物理优秀率分别为
分为优秀.若该班数学优秀率与物理优秀率分别为![]() 和
和![]() ,且除去抽走的
,且除去抽走的![]() 名同学外,剩下的同学中数学优秀但物理不优秀的同学共有
名同学外,剩下的同学中数学优秀但物理不优秀的同学共有![]() 人,请写出
人,请写出![]() 列联表,判断能否在犯错误的概率不超过
列联表,判断能否在犯错误的概率不超过![]() 的前提下认为数学优秀与物理优秀有关?
的前提下认为数学优秀与物理优秀有关?
参考数据: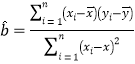 ,
,![]() ;
;![]() ,
,![]() ;
;![]()