题目内容
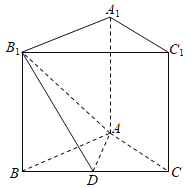
【题目】如图，多面体ABCD﹣A1B1C1D1为正方体，则下面结论正确的是（ ）
A.A1B∥B1C
B.平面CB1D1⊥平面A1B1C1D1
C.平面CB1D1∥平面A1BD
D.异面直线AD与CB1所成的角为30°
【答案】C
【解析】
根据正方体的顶点位置，可判断A1B、B1C是异面直线；平面CB1D1内不存在与平面A1B1C1D1
垂直的直线，平面A1B1C1D1内不存在直线垂直平面CB1D1，平面CB1D1不垂直平面A1B1C1D1；根据面面平行的判断定理可证平面CB1D1∥平面A1BD；根据正方体边的平行关系，可得异面直线AD与CB1所成的角为45°，即可得出结论.
选项A:
平面
平面
平面
，
是异面直线，该选项不正确；
选项B:由正方体可知
，
平面
，
平面
，
同理
平面
，
而平面
内不存在与
平行的直线，
所以平面内不存在直线垂直平面CB1D1；
同理平面CB1D1内不存在垂直平面A1B1C1D1的直线，
所以平面CB1D1不垂直平面A1B1C1D1，故该选项不正确；
选项C：由正方体可得
，可证
平面，
同理可证
平面，根据面面平行的判断定理
可得平面CB1D1∥平面A1BD，故该选项正确；
选项D: 
，异面直线AD与CB1所成的角为
而
，故该选项不正确.
故选:C
练习册系列答案
相关题目
