题目内容
.已知直线 与圆
与圆 相离,则三条边长分别为
相离,则三条边长分别为 、
、 、
、 的三角形是
的三角形是
| A.锐角三角形 | B.直角三角形 | C.钝角三角形 | D.以上均有可能 |
C
解析试题分析:因为已知中直线 与圆
与圆 相离,那么圆心为原点,则其到直线的距离为
相离,那么圆心为原点,则其到直线的距离为 ,那么根据余弦定理中三边的关系可知,角C为钝角,因此三条边长分别为
,那么根据余弦定理中三边的关系可知,角C为钝角,因此三条边长分别为 、
、 、
、 的三角形是钝角三角形,故选C.
的三角形是钝角三角形,故选C.
考点:本试题考查了直线与圆的位置关系。
点评:解决该试题的关键是得到a,b,c的关系式,进而确定三角形的形状,主要是看平方和之间的运算符号即可,属于基础题。

练习册系列答案
相关题目
在 中,内角
中,内角 所对的边分别为
所对的边分别为 ,
, ,则
,则 ( )
( )
A. | B. | C. | D. |
 中,若
中,若 ,则
,则 的值为
的值为
| A.2 | B.4 | C. | D.2 |
若∆ABC的三个内角成等差数列,三边成等比数列,则∆ABC是
| A.直角三角形 | B.等腰直角三角形 | C.等边三角形 | D.钝角三角形 |
已知 ,则A= ( )
,则A= ( )
A. | B. | C. | D. |
在△ 中,
中, 分别是角
分别是角 的对边,且
的对边,且 ,若
,若 =
= ,
, ,则△
,则△ 的面积为( )
的面积为( )
A. | B. | C. | D. |
在△ 中,若
中,若 ,则
,则 等于( )
等于( )
A. | B. | C. | D. |
 的取值范围是
的取值范围是 ) C.(1,
) C.(1,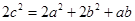 ,则△ABC是( )
,则△ABC是( )