题目内容
已知函数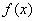 的定义域为
的定义域为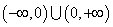 ,且满足条件:①
,且满足条件:①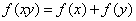 ;②
;②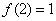 ;③当
;③当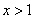 时,
时, .(1)求证:
.(1)求证: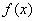 为偶函数;(2)讨论函数的单调性;(3)求不等式
为偶函数;(2)讨论函数的单调性;(3)求不等式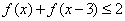 的解集.
的解集.
(1)证明:令x=y=1 有f(1)=f(1)+f(1) ∴f(1)=0
令x=y=-1 有f(1)=f(-1)+f(-1) ∴f(-1)=0
令y=-1 有f(-x)=f(x)+f(-1) ∴f(x)=f(-x)且定义域关于原式对称
∴f(x)是偶函数 法二:f(x2)=f(x)+f(x)
=f(-x)+f(-x)
∴f(x)=f(-x)
法三:令y=-1
f(-x)=f(x)+f(-1) ①
x=-x y=-1 f(x)=f(-x)+f(-1) ②
①-②
∴f(x)=f(-x)
(2)任取x1,x2∈(0,+ ∞)且x1<x2,则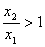
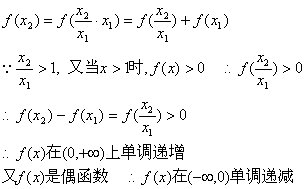
(3)
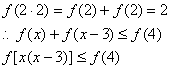
∵f(x)是偶函数
∴f(|x(x-3)|) ≤f(4)
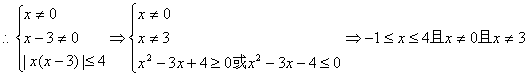
∴解集为[-1,0)∪(0,3)∪(3,4]

 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案 =
= ,
, ,
, = .
= .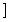 ∪[3,+∞) D.(-∞,-3
∪[3,+∞) D.(-∞,-3 的单调减区间是 ( )
的单调减区间是 ( ) B.
B.  C.
C.  D.
D. 
 ,
, ,则
,则 中,面对角线与
中,面对角线与 成
成 角的有
角的有 的三个顶点坐标为
的三个顶点坐标为 ,则
,则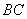 边上高线的长为__________。
边上高线的长为__________。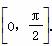 .
.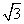 ),求|a+c|的最大值.
),求|a+c|的最大值. 解集为{x|x<-3,或x>-2},求k的值;
解集为{x|x<-3,或x>-2},求k的值;