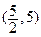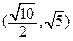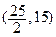题目内容
(本题满分12分)
已知离心率为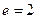 的双曲线
的双曲线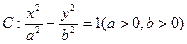 ,双曲线
,双曲线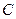 的一个焦点到
的一个焦点到
渐近线的距离是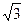
(1)求双曲线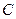 的方程
的方程
(2)过点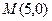 的
的 直线
直线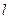 与双曲线
与双曲线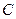 交于
交于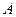 、
、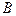 两点,交
两点,交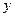 轴于
轴于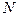 点
点 ,当
,当
 ,且
,且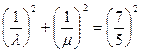 时,求直线
时,求直线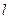 的方程
的方程
已知离心率为
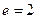 的双曲线
的双曲线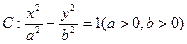 ,双曲线
,双曲线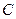 的一个焦点到
的一个焦点到渐近线的距离是
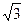
(1)求双曲线
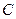 的方程
的方程(2)过点
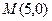 的
的 直线
直线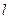 与双曲线
与双曲线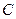 交于
交于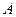 、
、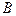 两点,交
两点,交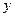 轴于
轴于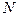 点
点 ,当
,当 ,且
,且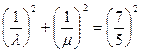 时,求直线
时,求直线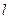 的方程
的方程解:(1) ………………………………………1分
………………………………………1分
右焦点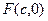 到渐近线
到渐近线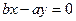 的距离
的距离
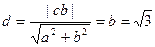 ………………………………3分
………………………………3分
从而得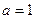
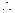 双曲线方程是
双曲线方程是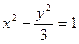 ………………………5分
………………………5分
(2)设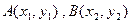 ,直线
,直线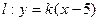 ,则
,则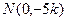
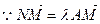
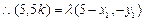
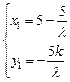
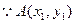 是双曲线
是双曲线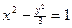 上的点
上的点
整理得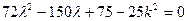 同理
同理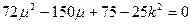 ……9分
……9分
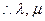 是方程
是方程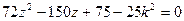 的两个
的两个 根
根
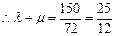 ,
, 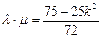 …………①
…………①
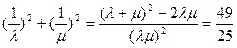 …………………②
…………………②
①代入② 解得
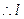 方程为
方程为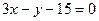 或
或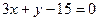 ……………………………12分
……………………………12分
解法二:设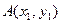 ,
,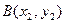
由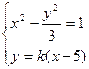 得
得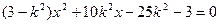
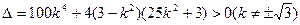 ………………①
………………①
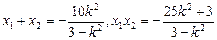
由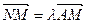 得
得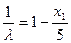 ,同理
,同理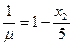
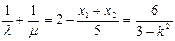 ,
,
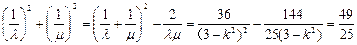
解得 满足①
满足①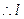 方程为
方程为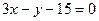 或
或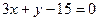
 ………………………………………1分
………………………………………1分右焦点
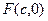 到渐近线
到渐近线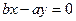 的距离
的距离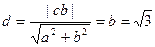 ………………………………3分
………………………………3分从而得
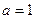
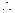 双曲线方程是
双曲线方程是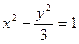 ………………………5分
………………………5分(2)设
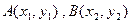 ,直线
,直线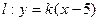 ,则
,则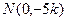
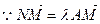
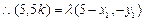
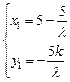
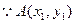 是双曲线
是双曲线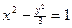 上的点
上的点
整理得
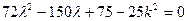 同理
同理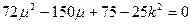 ……9分
……9分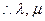 是方程
是方程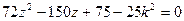 的两个
的两个 根
根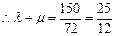 ,
, 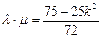 …………①
…………①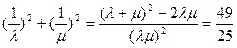 …………………②
…………………②①代入② 解得

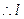 方程为
方程为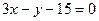 或
或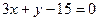 ……………………………12分
……………………………12分解法二:设
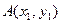 ,
,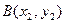
由
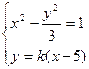 得
得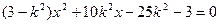
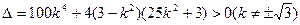 ………………①
………………①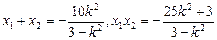
由
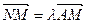 得
得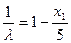 ,同理
,同理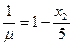
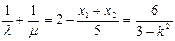 ,
,
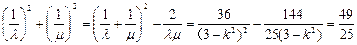
解得
 满足①
满足①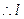 方程为
方程为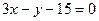 或
或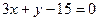
略

练习册系列答案
相关题目
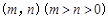 ,且渐近线方程为
,且渐近线方程为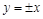 ,则双曲线的焦点( )
,则双曲线的焦点( )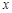 轴上
轴上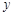 轴上
轴上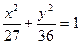 有相同焦点,且经过点
有相同焦点,且经过点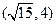 ,求双曲线的方程
,求双曲线的方程
 的离心率
的离心率 ,过点
,过点 和
和 的直线与原点的距离为
的直线与原点的距离为 .
. 与该双曲线交于不同的两点
与该双曲线交于不同的两点 ,且
,且 为圆心的同一圆上,求
为圆心的同一圆上,求 的取值范围.
的取值范围.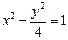 的两条渐近线和直线
的两条渐近线和直线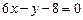 所围成三角形的边界及内部。当
所围成三角形的边界及内部。当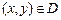 时,
时,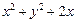 的最大值为( )
的最大值为( )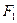 、
、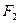 是双曲线
是双曲线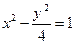 的左、右两个焦点,若双曲线右支上存在一点P,使
的左、右两个焦点,若双曲线右支上存在一点P,使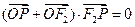 (O为坐标原点)且
(O为坐标原点)且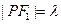
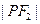 则
则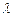 的值为( )
的值为( )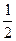
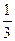
 的两条渐近线分别为
的两条渐近线分别为 F为其右焦点,过F作
F为其右焦点,过F作 交双曲线于点M,交《于7V,若
交双曲线于点M,交《于7V,若 ,且
,且 ,则双曲线的离心率的取值范围为
,则双曲线的离心率的取值范围为



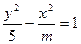 的离心率
的离心率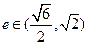 ,则m的取值范围是
,则m的取值范围是