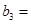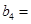题目内容
已知 是定义在
是定义在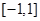 上的奇函数,且
上的奇函数,且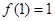 ,若
,若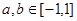 ,
,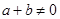 有
有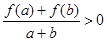 恒成立.
恒成立.
(1)判断 在
在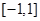 上是增函数还是减函数,并证明你的结论;
上是增函数还是减函数,并证明你的结论;
(2)若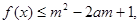 对所有
对所有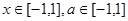 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
(1)见解析(2) .
.
解析试题分析:(1)先在定义域内取 ,然后用作差法判断出
,然后用作差法判断出 ,根据单调性的定义即可得到结果.(2)转化不等式为
,根据单调性的定义即可得到结果.(2)转化不等式为 ,
, ,再看成关于a的一次函数,满足
,再看成关于a的一次函数,满足 即可得到结果.
即可得到结果.
(1)增函数,
证明: 设


由题知:

(2) 由(1)知 
要使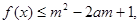 对所有
对所有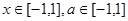 恒成立
恒成立 ,即
,即
令 只要
只要 :
:
考点:单调性的判断方法;恒成立问题;

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
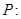 函数
函数 在区间
在区间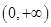 上是单调递增函数;命题
上是单调递增函数;命题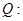 不等式
不等式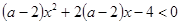 对任意实数
对任意实数 恒成立.若
恒成立.若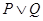 是真命题,且
是真命题,且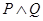 为假命题,求实数
为假命题,求实数 的取值范围.
的取值范围.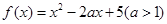 .
. 的定义域和值域均是
的定义域和值域均是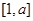 ,求实数
,求实数 的值;
的值;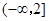 上是减函数,且对任意的
上是减函数,且对任意的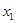 ,
,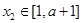 ,总有
,总有 ,求实数
,求实数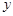 (千辆/时)与汽车的平均速度
(千辆/时)与汽车的平均速度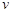 (千米/时)之间的函数关系为
(千米/时)之间的函数关系为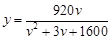 (
(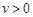 ).
).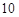 千辆/时,则汽车的平均速度应在什么范围内?
千辆/时,则汽车的平均速度应在什么范围内?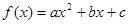 (a≠0)满足
(a≠0)满足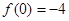 ,
,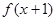 为偶函数,且x=-2是函数
为偶函数,且x=-2是函数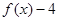 的一个零点.又
的一个零点.又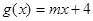 (
( >0).
>0).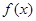 的解析式;
的解析式;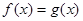 在
在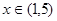 上有解,求实数
上有解,求实数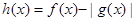 ,求
,求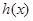 的单调区间.
的单调区间.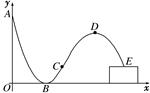
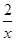 且f(4)=
且f(4)=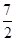 .
. 轴上的椭圆
轴上的椭圆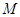 的离心率为
的离心率为 ,椭圆上异于长轴顶点的任意点
,椭圆上异于长轴顶点的任意点 与左右两焦点
与左右两焦点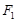 、
、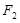 构成的三角形中面积的最大值为
构成的三角形中面积的最大值为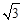 .
.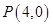 ,连接
,连接 与椭圆的另一交点记为
与椭圆的另一交点记为 ,若
,若 与椭圆的另一交点记为
与椭圆的另一交点记为 ,求
,求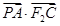 的取值范围.
的取值范围.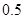 万张,同时规定一旦某年发放的牌照超过15万张,以后每一年发放的电动车的牌照的数量维持在这一年的水平不变.
万张,同时规定一旦某年发放的牌照超过15万张,以后每一年发放的电动车的牌照的数量维持在这一年的水平不变.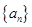 ,每年发放的电动型汽车牌照数为构成数列
,每年发放的电动型汽车牌照数为构成数列 ,完成下列表格,并写出这两个数列的通项公式;
,完成下列表格,并写出这两个数列的通项公式;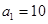
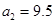
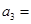

 3
3