题目内容
已知函数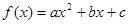 (a≠0)满足
(a≠0)满足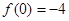 ,
,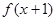 为偶函数,且x=-2是函数
为偶函数,且x=-2是函数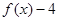 的一个零点.又
的一个零点.又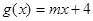 (
( >0).
>0).
(1)求函数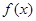 的解析式;
的解析式;
(2)若关于x 的方程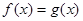 在
在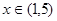 上有解,求实数
上有解,求实数 的取值范围;
的取值范围;
(3)令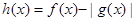 ,求
,求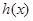 的单调区间.
的单调区间.
(1)函数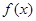 的解析式为
的解析式为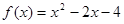 ; (2)实数
; (2)实数 的取值范围为
的取值范围为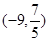 ;
;
(3)当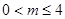 时,
时,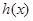 的单调递减区间为
的单调递减区间为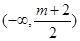 ,单调递增区间为
,单调递增区间为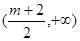 ;
;
当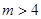 时,
时,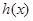 的单调递减区间为
的单调递减区间为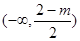 和
和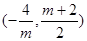 ;
;
单调递增区间为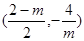 和
和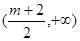 .
.
解析试题分析:(1)由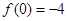 得
得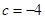 ,又
,又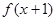 为偶函数,
为偶函数,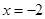 是函数
是函数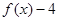 的一个零点,得出关于
的一个零点,得出关于 的方程,即可求函数
的方程,即可求函数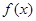 的解析式;
的解析式;
(2)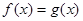 在
在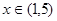 上有解,等价于
上有解,等价于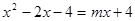 在
在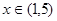 上有解,可求实数
上有解,可求实数 的取值范围;
的取值范围;
(3)先求出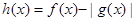 的解析式,再分
的解析式,再分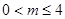 、
、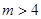 两种情况求出
两种情况求出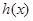 的单调区间.
的单调区间.
(1)由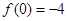 得
得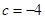 1分
1分
∵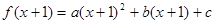 即
即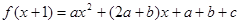
又∵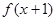 为偶函数 ∴
为偶函数 ∴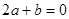 ① 2分
① 2分
∵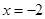 是函数
是函数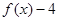 的一个零点 ∴
的一个零点 ∴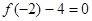 ∴
∴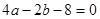 ②
②
解①②得a=1,b=-2
∴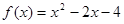 4分
4分
(2)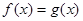 在
在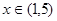 上有解,即
上有解,即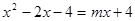 在
在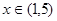 上有解.
上有解.
∴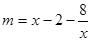
∵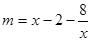 在
在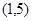 上单调递增
上单调递增
∴实数 的取值范围为
的取值范围为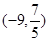 8分
8分
(3)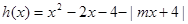 即
即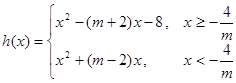 9分
9分
①当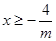 时,
时,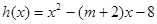 的对称轴为
的对称轴为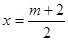
∵m>0 ∴ 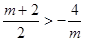 总成立
总成立
∴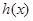 在
在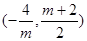 单调递减,在
单调递减,在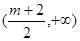 上单调递增. 11分
上单调递增. 11分
②当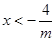 时,
时,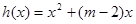 的对称轴为
的对称轴为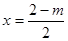
若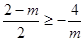 即
即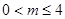 ,
,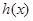 在
在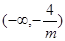 单调递减 13分
单调递减 13分
若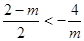 即
即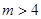 ,
,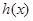 在
在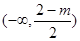 单调递减,在
单调递减,在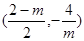 上单调递增. 15分
上单调递增. 15分
综上,
当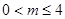 时,
时,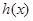

练习册系列答案
 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目
有一种密英文的明文(真实文)按字母分解,其中英文的a,b,c, ,z的26个字母(不分大小写),依次对应1,2,3, ,26这26个自然数,见如下表格:
| a | b | c | d | e | f | g | h | i | j | k | l | m |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 |
| n | o | p | q | r | s | t | u | v | w | x | y | z |
| 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 |
给出如下变换公式:
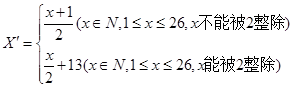
将明文转换成密文,如
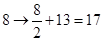 ,即
,即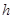 变成
变成 ;如
;如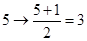 ,即
,即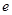 变成
变成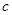 .
.(1)按上述规定,将明文
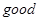 译成的密文是什么?
译成的密文是什么?(2)按上述规定,若将某明文译成的密文是
 ,那么原来的明文是什么?
,那么原来的明文是什么? 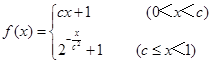 ,且
,且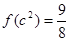 .
.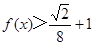 .
.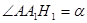 .
.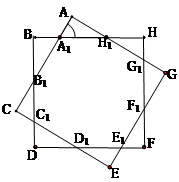
 表示
表示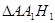 的面积;
的面积; 是定义在
是定义在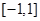 上的奇函数,且
上的奇函数,且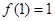 ,若
,若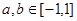 ,
,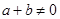 有
有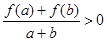 恒成立.
恒成立.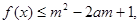 对所有
对所有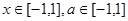 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.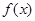 满足对任意的
满足对任意的 恒有
恒有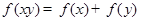 ,且当
,且当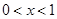 时,
时,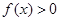 .
.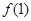 的值;
的值;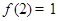 ,解不等式
,解不等式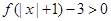 .
.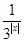 .
.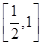 恒成立,求m的取值范围.
恒成立,求m的取值范围.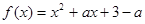 ,
,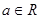 .
. 的取值范围,使
的取值范围,使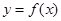 在闭区间
在闭区间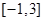 上是单调函数;
上是单调函数;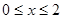 时,函数
时,函数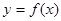 的最大值是关于
的最大值是关于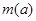 .求
.求
 ,恒有
,恒有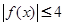 成立.
成立. 的值域为________________________.
的值域为________________________.