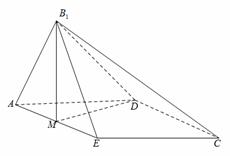
题目内容
如图,已知等腰梯形 中,
中,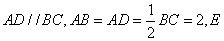 是
是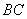 的中点,
的中点,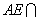
 ,将
,将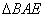 沿着
沿着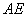 翻折成
翻折成 ,使平面
,使平面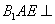 平面
平面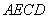 .
.
(I) 求证: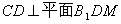 ;
;
(II)求二面角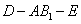 的余弦值;
的余弦值;
(III)在线段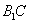 上是否存在点P,使得
上是否存在点P,使得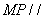 平面
平面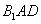 ,若存在,求出
,若存在,求出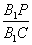 的值;若不存在,说明理由.
的值;若不存在,说明理由.
|
( I ) 由题意可知四边形 是平行四边形,所以
是平行四边形,所以 ,故
,故 .
.
又因为 所以
所以 ,
,
即
 ,
,
所以四边形 是平行四边形.
是平行四边形.
所以
故 .
.
因为平面 平面
平面 , 平面
, 平面 平面
平面 ,
, 平面
平面
所以 平面
平面 .
.
因为 平面
平面 , 所以
, 所以
 .
.
因为 ,
,  、
、 平面
平面 ,
,
所以 平面
平面 . ……………5分
. ……………5分
 (II) 以
(II) 以 为
为 轴,
轴,  为
为 轴,
轴,  为
为 轴建立空间直角坐标系,则
轴建立空间直角坐标系,则 ,
,  ,
,  ,
,  .
.
平面 的法向量为
的法向量为 .
.
设平面 的法向量为
的法向量为 , 因为
, 因为 ,
, ,
,
 , 令
, 令 得,
得,  .
.
所以 , 因为二面角
, 因为二面角 为锐角,
为锐角,
所以二面角 的余弦值为
的余弦值为 . ……………10分
. ……………10分
(III) 存在点P,使得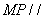 平面
平面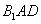 . ……………11分
. ……………11分
法一: 取线段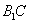 中点P,
中点P, 中点Q,连结
中点Q,连结 .
.
|

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目
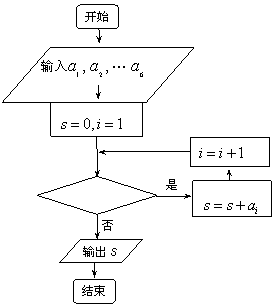
在篮球比赛中,某篮球队队员投进三分球的个数如表所示:
| 队员i | 1 | 2 | 3 | 4 | 5 | 6 |
| 三分球个数 |
|
|
|
|
|
|
右图是统计上述6名队员在比赛中投进的三分球总数s的程序框图,则图中的判断框内应填入的条件是
A. 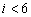 B.
B.  C.
C. 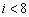 D.
D. 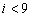


 与直线
与直线 有两个不同的交点时,则实数k的取值范围是 ( )
有两个不同的交点时,则实数k的取值范围是 ( ) B.
B. C.
C.  D.
D. 








 是有序数对集合
是有序数对集合 上的一个映射,正整数数对
上的一个映射,正整数数对 ,记作
,记作 . 对于任意的正整数
. 对于任意的正整数 ,映射
,映射 的解集为
的解集为 






 ,
, ,
,  为
为 的值是 .
的值是 . 
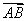 ·
· =
= ·
· =1,那么c=____
=1,那么c=____ ____.
____. =(2x+3,-x),x∈R.
=(2x+3,-x),x∈R.