题目内容
已知函数f（x）=sinx-cosx且f′（x）是f（x）的导函数，若f′（α）=2f（α），则tan2α=______．
∵f（x）=sinx-cosx，
∴f'（x）=cosx+sinx，
∵f′（α）=2f（α），
∴cosα+sinα=2（sinα-cosα），
即sinα=3cosα，
∴tanα=3，
∴tan2α=
=
=
=-
，
故答案为：-
；
∴f'（x）=cosx+sinx，
∵f′（α）=2f（α），
∴cosα+sinα=2（sinα-cosα），
即sinα=3cosα，
∴tanα=3，
∴tan2α=
| 2tanα |
| 1-tan2α |
| 6 |
| 1-32 |
| 6 |
| -8 |
| 3 |
| 4 |
故答案为：-
| 3 |
| 4 |
练习册系列答案
相关题目
．
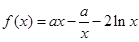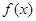在
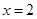时有极值，求实数
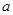的值和
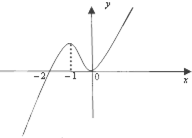
，若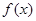
存在唯一的零点
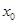，且
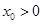，则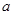
的取值范围是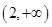
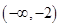
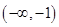
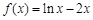的单调递减区间是 .