题目内容
11.函数f(x)=eax-$\frac{1}{a}$lnx(a>0)存在零点,则实数a的取值范围是( )| A. | 0<a≤$\frac{1}{e}$ | B. | 0<a≤$\frac{1}{{e}^{2}}$ | C. | a≥$\frac{1}{e}$ | D. | a≥$\frac{1}{{e}^{2}}$ |
分析 先考虑函数f(x)=ax与g(x)=logax(a>1)图象仅有一个交点,且在公共点处有公共的切线,a的值,再利用换元法,即可得出结论.
解答 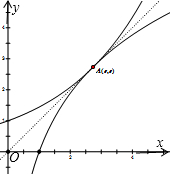 解:先考虑函数f(x)=ax与g(x)=logax(a>1)图象仅有一个交点,
解:先考虑函数f(x)=ax与g(x)=logax(a>1)图象仅有一个交点,
且在公共点处有公共的切线,a的值.
两函数互为反函数,则该切线即为y=x,设切点A,
可求出A(e,e),此时a=e${\;}^{\frac{1}{e}}$.
若a>e${\;}^{\frac{1}{e}}$时,则f(x)=ax与g(x)=logax(a>1)无公共点;
若1<a<e${\;}^{\frac{1}{e}}$时,则f(x)=ax与g(x)=logax(a>1)有两个公共点.
对f(x)=eax-$\frac{1}{a}$lnx(a>0),换元令t=ea,即得tx=logtx,
由上知1<ea=t≤e${\;}^{\frac{1}{e}}$,得0<a≤$\frac{1}{e}$.
故选:A.
点评 本题考查函数的零点,考查数形结合的数学思想,考查学生转化问题的能力,属于中档题.

练习册系列答案
相关题目
6.已知f(x)=$\left\{\begin{array}{l}{\frac{2}{x},x≥2}\\{(x-1)^{3},x<2}\end{array}\right.$,若函数g(x)=f(x)-k有两个零点,则两零点所在的区间为( )
| A. | (-∞,0) | B. | (0,1) | C. | (1,2) | D. | (1,+∞) |
3.利用计算机在区间(0,1)上产生随机数a,则不等式0<log2(3a-1)<1成立的概率是( )
| A. | $\frac{1}{2}$ | B. | $\frac{2}{3}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{4}$ |
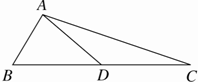 如图,在△ABC中,BC边上的中线AD长为3,且cosB=$\frac{\sqrt{10}}{8}$,cos∠ADC=-$\frac{1}{4}$.
如图,在△ABC中,BC边上的中线AD长为3,且cosB=$\frac{\sqrt{10}}{8}$,cos∠ADC=-$\frac{1}{4}$.