题目内容
6.已知f(x)=$\left\{\begin{array}{l}{\frac{2}{x},x≥2}\\{(x-1)^{3},x<2}\end{array}\right.$,若函数g(x)=f(x)-k有两个零点,则两零点所在的区间为( )| A. | (-∞,0) | B. | (0,1) | C. | (1,2) | D. | (1,+∞) |
分析 求得x≥2时,x<2时,可得函数f(x)的单调性和值域,即有y=f(x)的图象和直线y=k有两个交点.通过图象观察,即可得到所求区间.
解答 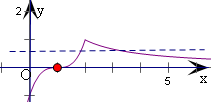 解:f(x)=$\left\{\begin{array}{l}{\frac{2}{x},x≥2}\\{(x-1)^{3},x<2}\end{array}\right.$,可得x≥2时,f(x)=$\frac{2}{x}$递减,且f(x)∈(0,1];
解:f(x)=$\left\{\begin{array}{l}{\frac{2}{x},x≥2}\\{(x-1)^{3},x<2}\end{array}\right.$,可得x≥2时,f(x)=$\frac{2}{x}$递减,且f(x)∈(0,1];
当x<2时,f(x)=(x-1)3递增,且f(x)∈(-∞,1).
画出函数f(x)的图象,如图:
令g(x)=f(x)-k=0,即有y=f(x)的图象和直线y=k有两个交点.
由图象可得,当0<k<1时,直线y=k和y=f(x)有两个交点,
可得函数g(x)=f(x)-k的两个零点在(1,+∞).
故选:D.
点评 本题考查分段函数的图象及应用,考查函数方程的转化思想,注意运用数形结合的思想方法,属于基础题.

练习册系列答案
 高中必刷题系列答案
高中必刷题系列答案
相关题目
6.一个三角形的三边成等比数列,则公比q的范围是( )
| A. | q>$\frac{\sqrt{5}+1}{2}$ | B. | q<$\frac{\sqrt{5}-1}{2}$ | C. | $\frac{\sqrt{5}-1}{2}$<q<$\frac{\sqrt{5}+1}{2}$ | D. | q<$\frac{\sqrt{5}-1}{2}$或q>$\frac{\sqrt{5}+1}{2}$ |
7.下列四个数中数值最大的是( )
| A. | 1111(2) | B. | 16 | C. | 23(7) | D. | 30(6) |
11.函数f(x)=eax-$\frac{1}{a}$lnx(a>0)存在零点,则实数a的取值范围是( )
| A. | 0<a≤$\frac{1}{e}$ | B. | 0<a≤$\frac{1}{{e}^{2}}$ | C. | a≥$\frac{1}{e}$ | D. | a≥$\frac{1}{{e}^{2}}$ |
 如图,在直三棱柱ABC-A1B1C1中,AC=3,BC=4,AB=5,AA1=4,点D是AB的中点.
如图,在直三棱柱ABC-A1B1C1中,AC=3,BC=4,AB=5,AA1=4,点D是AB的中点.