Question

设不等式|x+1|-|x-2|＞k的解集为R,求实数k的取值范围.

Answer 1

解法一：根据绝对值的几何意义,|x+1|可以看作数轴上点P(x)到点A(-1)的距离|PA|,|x-2|可以看作是数轴上点P(x)到点B(2)的距离|PB|,则|x+1|-|x-2|=|PA|-|PB|.如图所示:

当点P在线段AB上时,-3≤|PA|-|PB|≤3,

当P在A点左侧时,|PA|-|PB|=-3,

当P在B点右侧时,|PA|-|PB|=3,

则不等式-3≤|x+1|-|x-2|≤3恒成立.

故使原不等式的解集为R的实数k的取值范围是k＜-3.

解法二:令y=|x+1|-|x-2|

=

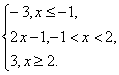
在直角坐标系中,作出函数图象如图.

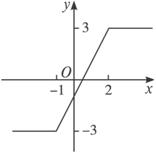
要使不等式|x+1|-|x-2|＞k对一切实数成立,则函数图象全部都落在直线y=k的上方,则k的取值范围为k＜

-3.