题目内容
已知m∈R,设条件p:不等式(m2-1)x2+(m+1)x+1≥0对任意的x∈R恒成立;条件q:关于x的不等式|x+1|+|x-2|<m的解集为Φ.
(1)分别求出使得p以及q为真的m的取值范围;
(2)若复合命题“p或q”为真,“p且q”为假,求实数m的取值范围.
(1)分别求出使得p以及q为真的m的取值范围;
(2)若复合命题“p或q”为真,“p且q”为假,求实数m的取值范围.
分析:本题考查的知识点是复合命题的真假判定,解决的办法是先判断组成复合命题的简单命题的真假,再根据真值表进行判断.
解答:解:(1)∵p:不等式(m2-1)x2+(m+1)x+1≥0对任意的x∈R恒成立
当p为真时,
∴m=-1或
?m≤-1或m≥
又∵q:关于x的不等式|x+1|+|x-2|<m的解集为Φ
当q为真,
∴(|x+1|+|x-2|)min≥m?m≤3,
∴p真时m的取值范围为A={m|m≤-1或m≥
},q真时m的取值范围为B={m|m≤3};
(2)∵“p或q”为真,“p且q”为假,
∴p和q一真一假,分两况讨论:
1°当p真且q假时,有A∩CRB={m|m>3};
2°当p假且q真时,有(CRA)∩B={m|-1<m<
},
1°,2°取并,
即得“p或q”为真,“p且q”为假时实数m的取值范围是{m|-1<m<
或m>3}
当p为真时,
∴m=-1或
|
| 5 |
| 3 |
又∵q:关于x的不等式|x+1|+|x-2|<m的解集为Φ
当q为真,
∴(|x+1|+|x-2|)min≥m?m≤3,
∴p真时m的取值范围为A={m|m≤-1或m≥
| 5 |
| 3 |
(2)∵“p或q”为真,“p且q”为假,
∴p和q一真一假,分两况讨论:
1°当p真且q假时,有A∩CRB={m|m>3};
2°当p假且q真时,有(CRA)∩B={m|-1<m<
| 5 |
| 3 |
1°,2°取并,
即得“p或q”为真,“p且q”为假时实数m的取值范围是{m|-1<m<
| 5 |
| 3 |
点评:本题考查的知识点是复合命题的真假判定,属于基础题目

练习册系列答案
 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案
相关题目
已知O为平面内一定点,设条件p:动点M满足
=
+λ(
+
),λ∈R;条件q:点M的轨迹通过△ABC的重心.则条件p是条件q的( )
| OM |
| OA |
| AB |
| AC |
| A、充要条件 |
| B、充分不必要条件 |
| C、必要不充分条件 |
| D、既不充分也不必要条件 |

 ,m
,m 0),点P的轨迹加上M、N两点构成曲线C.
0),点P的轨迹加上M、N两点构成曲线C. ,曲线C过点Q (2,0) 斜率为
,曲线C过点Q (2,0) 斜率为 的直线
的直线 与曲线C交于不同的两点A﹑B,AB中点为R,直线OR (O为坐标原点)的斜率为
与曲线C交于不同的两点A﹑B,AB中点为R,直线OR (O为坐标原点)的斜率为 ,求证
,求证  为定值;
为定值; ,且
,且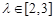 ,求
,求