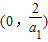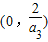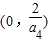题目内容
0<a1<a2<a3,则使得(1-aix)2<1(i=1,2,3)都成立的实数x的取值范围是
(0,
)
| 2 |
| a3 |
(0,
)
.| 2 |
| a3 |
分析:先解出不等式(1-aix)2<1的解集,再由0<a1<a2<a3,确定实数x的取值范围.
解答:解:由题意,(1-aix)2<1?-1<1-aix<1?0<x<
恒成立.
∵0<a1<a2<a3,∴
>
>
∴x∈(0,
)
故答案为(0,
)
| 2 |
| ai |
∵0<a1<a2<a3,∴
| 2 |
| a1 |
| 2 |
| a2 |
| 2 |
| a3 |
∴x∈(0,
| 2 |
| a3 |
故答案为(0,
| 2 |
| a3 |
点评:本题的考点是函数恒成立问题,主要考查解一元二次不等式.考查不等式恒成立问题的转化策略,属基础题.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
在数列{an}中an≠0,a1,a2,a3成等差数列,a2,a3,a4成等比数列,a3,a4,a5的倒数成等差数列,则a1,a3,a5( )
| A、是等差数列 | B、是等比数列 | C、三个数的倒数成等差数列 | D、三个数的平方成等差数列 |

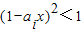 (i=1,2,3,4)都成立的x的取值范围是( )
(i=1,2,3,4)都成立的x的取值范围是( )