题目内容
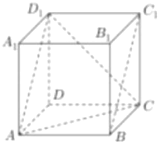
【题目】如图，正方体
，则下列四个命题:
①点
在直线
上运动，三棱锥
的体积不变
②点在直线上运动，直线
与平面
所成角的大小不变
③点在直线上运动，二面角
的大小不变
④点是平面
上到点
和
距离相等的动点，则的轨迹是过点
的直线.
其中的真命题是（ ）
A.①③B.①③④C.①②④D.③④
【答案】B
【解析】
①由正方体的性质，易知
平面
，因此直线
上的点到平面的距离不变，又
的面积不变，所以体积不变.②点
在直线上运动，
的大小在改变，所以直线与平面
所成角的大小改变，③点在直线上运动，两面的位置不变，所以二面角
的大小不变.④用向量法来判断，建立空间直角坐标系，设
，由
的方程来判断.
①由正方体的性质可得:
，于是平面，因此直线上的点到平面的距离不变，点在直线上运动，又的面积不变，因此三棱锥
的体积
不变.
②点在直线上运动，由①可知:直线上的点到平面的距离不变，而的大小在改变，因此直线与平面所成角的大小改变，故不正确.
③点在直线上运动，由①可知:点到平面的距离不变，点到
的距离不变，可得二面角的大小不变，正确；
④如图所示，
不妨设正方体的棱长为
，
，
，设，∵，则
，化为
，因此的轨迹是过点
的直线，正确.
其中真命题是①③④.
故选：B
练习册系列答案
小学期末标准试卷系列答案
相关题目
