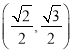题目内容
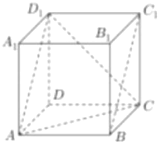
【题目】在我国古代数学名著《九章算术》中,将四个面都是直角三角形的四面体称为“鳖臑”,在鳖臑![]() 中,
中,![]() 平面
平面![]() ,且
,且![]() 为
为![]() 的中点,则异面直线
的中点,则异面直线![]() 与
与![]() 所成角的正弦值为( )
所成角的正弦值为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】D
【解析】
分析1:设![]() 是
是![]() 中点,连接
中点,连接![]() ,利用三角形中位线的性质,结合异面直线的定义,可知
,利用三角形中位线的性质,结合异面直线的定义,可知![]() 是两条异面直线所成的角.根据题中所给鳖臑的性质,结合勾股定理的逆定理求解即可;
是两条异面直线所成的角.根据题中所给鳖臑的性质,结合勾股定理的逆定理求解即可;
分析2:通过已知的线面垂直,可以得到线线垂直,再利用已知结合线面垂直的判定定理可以证明出![]() 平面
平面![]() ,进而求解即可.
,进而求解即可.
解法1:设![]() 是
是![]() 中点,连接
中点,连接![]() ,
,

由于![]() 分别是
分别是![]() 中点,
中点,![]() 是三角形
是三角形![]() 的中位线,
的中位线,
故![]() ,
,
![]() 是两条异面直线所成的角.
是两条异面直线所成的角.
不妨设![]()
根据鳖臑的几何性质可知![]() .
.
故![]() ,又
,又![]() ,在三角形
,在三角形![]() 中,
中,
![]()
故选![]()
解法2:![]() 平面
平面![]() 平面
平面![]() ,
,
又![]() ,
,![]() 平面
平面![]()
![]() 平面
平面![]() ,
,![]() 异面直线
异面直线![]() 与
与![]() 所成的角为直角,
所成的角为直角,
其正弦值为![]() .
.
故选:D

练习册系列答案
 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案
相关题目