题目内容
已知函数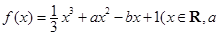 ,
,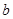 为实数)有极值,且在
为实数)有极值,且在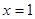 处的切线与直线
处的切线与直线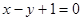 平行.
平行.
(Ⅰ)求实数a的取值范围;
(Ⅱ)是否存在实数a,使得函数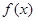 的极小值为1,若存在,求出实数a的值;若不存在,请说明理由;
的极小值为1,若存在,求出实数a的值;若不存在,请说明理由;
(Ⅲ)设函数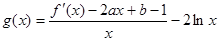 试判断函数
试判断函数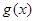 在
在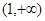 上的符号,并证明:
上的符号,并证明:
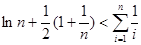 (
(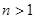 ).
).
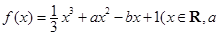 ,
,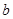 为实数)有极值,且在
为实数)有极值,且在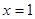 处的切线与直线
处的切线与直线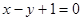 平行.
平行.(Ⅰ)求实数a的取值范围;
(Ⅱ)是否存在实数a,使得函数
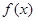 的极小值为1,若存在,求出实数a的值;若不存在,请说明理由;
的极小值为1,若存在,求出实数a的值;若不存在,请说明理由;(Ⅲ)设函数
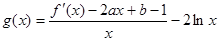 试判断函数
试判断函数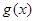 在
在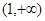 上的符号,并证明:
上的符号,并证明: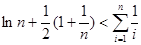 (
(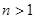 ).
).(Ⅰ)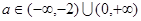 ;(Ⅱ)
;(Ⅱ)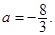 (Ⅲ)见解析.
(Ⅲ)见解析.
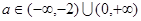 ;(Ⅱ)
;(Ⅱ)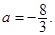 (Ⅲ)见解析.
(Ⅲ)见解析.试题分析:(Ⅰ)由已知在
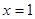 处的切线与直线
处的切线与直线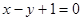 平行,得
平行,得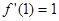 且
且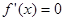 有两个不等实根,从而得出
有两个不等实根,从而得出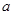 的范围;(Ⅱ)先由导函数得出函数的单调性,确定函数的极小值点,然后由函数
的范围;(Ⅱ)先由导函数得出函数的单调性,确定函数的极小值点,然后由函数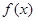 的极小值为1得出存在的
的极小值为1得出存在的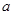 值;(Ⅲ)先确定
值;(Ⅲ)先确定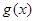 的单调性,
的单调性,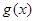 在
在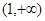 上是增函数,故
上是增函数,故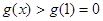 ,构造
,构造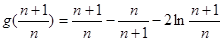
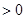 ,分别取
,分别取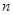 的值为1、2、3、 、
的值为1、2、3、 、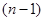 累加即可得证.
累加即可得证.试题解析:(Ⅰ)
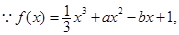
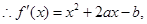 由题意
由题意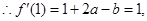
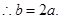 ① (1分)
① (1分)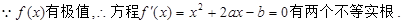
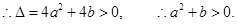 ②
②由①、②可得,
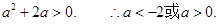
故实数a的取值范围是
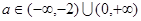 (3分)
(3分)(Ⅱ)存在
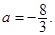 (5分)
(5分)由(1)可知
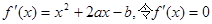 ,
,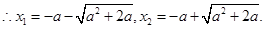 ,且
,且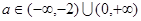
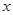 | 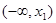 | 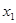 | 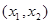 | 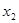 | 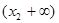 |
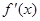 | + | 0 | - | 0 | + |
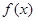 | 单调增 | 极大值 | 单调减 | 极小值 | 单调增 |
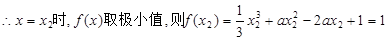 ,
,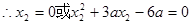 . (6分)
. (6分)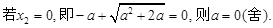 (7分)
(7分) 
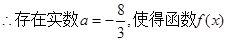 的极小值为1. (8分)
的极小值为1. (8分) (Ⅲ)由
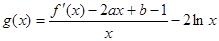
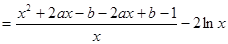
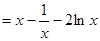
即
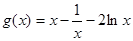
故,
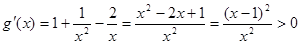
则
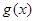 在
在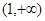 上是增函数,故
上是增函数,故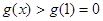 ,
,所以,
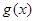 在
在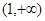 上恒为正。. (10分)
上恒为正。. (10分)(注:只判断符号,未说明理由的,酌情给分)
当
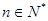 时,
时,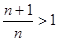 ,设
,设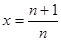 ,则
,则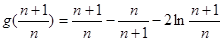
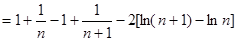
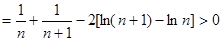
即:
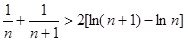 . (12分)
. (12分) 上式分别取
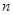 的值为1、2、3、 、
的值为1、2、3、 、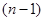 累加得:
累加得: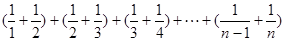
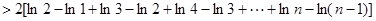 ,(
,(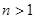 )
)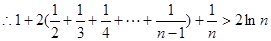 ,(
,(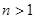 )
)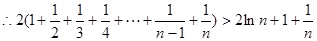 ,(
,(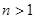 )
)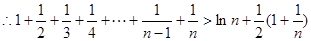 ,(
,(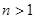 )
)即,
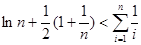 ,(
,(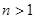 ),当
),当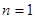 时也成立 (14分)
时也成立 (14分)
练习册系列答案
 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案
相关题目
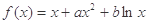 ,曲线
,曲线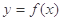 过点P(1,0),且在P点处的切斜线率为2.
过点P(1,0),且在P点处的切斜线率为2.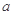 ,
,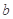 的值;
的值;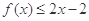 .
. 在点(1,1)处的切线方程为 .
在点(1,1)处的切线方程为 .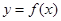 的图像为
的图像为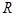 上的一条连续不断的曲线,当
上的一条连续不断的曲线,当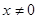 时,
时,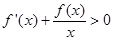 ,则关于
,则关于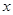 的函数
的函数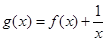 的零点的个数为( )
的零点的个数为( )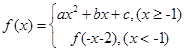 ,在其图象上点(
,在其图象上点(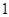 ,
,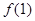 )处的切线方程为
)处的切线方程为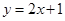 ,则图象上点(-
,则图象上点(-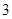 ,
,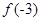 )处的切线方程为________________.
)处的切线方程为________________. 的图象上任意点处切线的倾斜则角为
的图象上任意点处切线的倾斜则角为 ,
,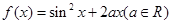 ,若对任意实数
,若对任意实数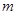 ,直线
,直线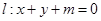 都不是曲线
都不是曲线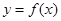 )的切线,则
)的切线,则
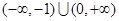

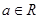 且
且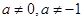
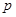 在曲线
在曲线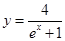 上,
上,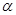 为曲线在点
为曲线在点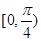
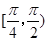
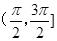

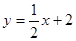 ,则
,则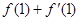 =______
=______